Почему минус на минус дает плюс?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
- сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
- умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
- сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.

Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Ответил: Евгений Епифанов
Плюс минус
Плюс минус
Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.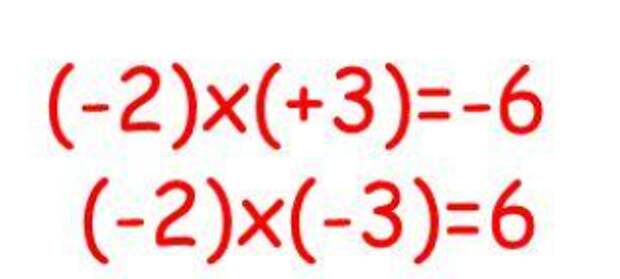
Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.
При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.
В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.
Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.
При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.
Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.
ВОПРОС — ОТВЕТ
«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке
(-6) : (-3) = +2
Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:
(-6) : (-3) = 2
«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.
13 ноября 2009 года — 22 сентября 2019 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
двойных отрицаний | Учебник по эффективному письму
Двойное отрицание — это выражение, содержащее два отрицательных слова.
Если в одном предложении используются два отрицания, может быть передано противоположное значение. Во многих британских, американских и других диалектах два или более отрицания могут использоваться с одним отрицательным значением.
| Неверно: | Я никого не видел. |
Однако английские и американские комментаторы употребления воспринимают двойную отрицательную форму как простоватую, необразованную и нестандартную. Вот более стандартная форма приведенного выше примера:
Правило для запоминания
Двойное отрицание — это утверждение, содержащее два отрицательных слова. Он не является частью стандартного английского языка, и его следует избегать.
Исправление двойных отрицаний
| Правильно: | Я никого не видел. |
Наиболее часто употребляемые отрицательные слова: нет, не, ничего, никогда, никто, никто, нигде, ни, и никто . Есть некоторые слова, которые имеют отрицательный элемент в своем значении, хотя они не содержат чрезмерно отрицательного аффикса. Эти слова: вряд ли, едва ли, едва, и т. д.
| Неправильно: | Я еще не успел подумать об экзамене. |
| Правильно: | Я едва начал думать об экзамене. |
Никто, ничего, никогда считаются эмфатичными. Будьте осторожны, когда используете эти слова. Используйте , а не кого-либо, никогда не используйте вместо этого .
Кто угодно, что угодно, и ever не являются отрицательными и должны использоваться с , а не с , чтобы передать отрицательное значение.
Допустимо использование двух отрицательных слов в предложении.
| Правильно: | Я никак не могу навестить маму в этом году. |
В приведенном выше предложении двойное отрицание используется эмфатически — «Я должен навестить свою мать».
Рассмотрим другой пример:
| Правильно: | Я не был недоволен своей оценкой. |
Здесь двойное отрицание используется для обозначения положительного или теплого значения — «Я не был недоволен, но и не был в восторге от своей оценки».
Две отрицательные идеи могут быть выражены союзами не… или и не. .. или . Когда 9За 0042 не следуют два или более глаголов, существительных или прилагательных, к ним присоединяются или .
.. или . Когда 9За 0042 не следуют два или более глаголов, существительных или прилагательных, к ним присоединяются или .
| Правильно: | Он не пьет и не танцует. |
Используйте или после фразы, чтобы отделить и подчеркнуть второй глагол, прилагательное или существительное.
| Правильно: | Наша главная цель не нефть и не электроэнергия. Это стабильность в регионе. |
Мисс имеет отрицательное значение и не требует добавления отрицательного.
| Неверно: | Я скучаю по тому, что не вижу его каждый день. |
| Правильно: | Я скучаю по нему каждый день. |
Есть несколько способов исправления двойного отрицания:
| Неверно: | Официантка только и делала, что курила. |
| Правильно: | Официантка только и делала, что курила. |
| Правильно: | Официантка ничего не делала, только курила. |
| Неправильно: | К концу дня у покупателя не осталось сил. |
| Правильно: | К концу дня у покупателя не осталось сил. |
| Правильно: | К концу дня у покупателя не осталось сил. |
Пройди тест
Предыдущий
Запоминающаяся чепуха «Два минуса делают позитив» — Математика с плохими рисунками
Бен Орлин
Образование
2 минуты
Мои ученики 6-го и 7-го классов довольно хорошо умеют считать с отрицательными числами. Все они знают, например, что 5 – (-2) = 7. Спросите их, почему, и вы услышите:
«Потому что два минуса дают плюс!»
Затем, если вы внимательно прислушаетесь, вы услышите кое-что еще: низкий рокот моих зубов, скрежещущих вместе с тектонической силой.
«Два минуса дают плюс» — один из тех математических лозунгов, который сводит меня с ума, потому что он такой содержательный, такой запоминающийся, такой простой в применении… и в то же время такой расплывчатый и не математический, что я поражаюсь, когда студенты находят это вообще полезно.
Мы все можем вспомнить множество случаев, когда два отрицательных числа не дают положительного числа. Дождь в день свадьбы плюс крупная кража в день вашей свадьбы не дают выигрышной комбинации, несмотря на то, что можно предположить, что «два минуса дают плюс».
Это неверно даже для отрицательных чисел, где -10 + -30 НЕ равно +40 (хотя я видел, как студенты утверждали, что это так, ссылаясь на то, что «два отрицательных значения дают положительное» в качестве своего обоснования).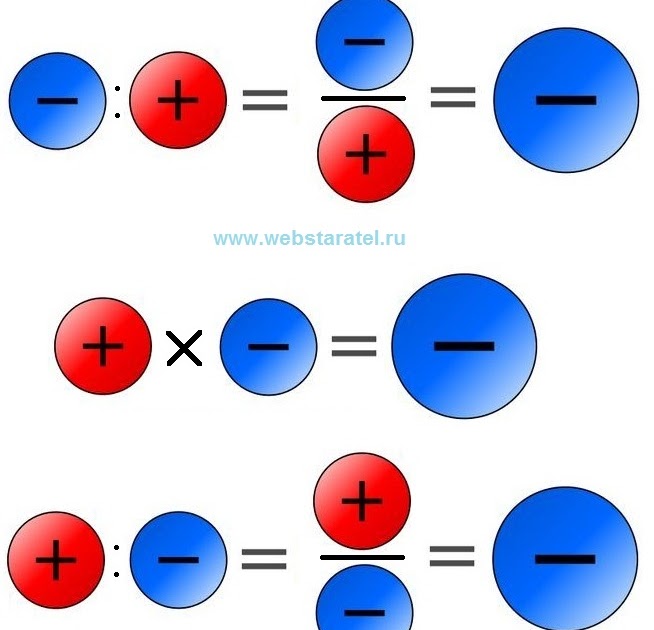
На самом деле, это одна из моих главных претензий к фразе «два отрицания дают положительный результат»: это настолько быстрое всеобъемлющее обобщение, что студенты начинают применять его в тех местах, где оно не имеет особого смысла.
На самом деле, «два минуса дают плюс» не имеет особого смысла везде .
Что действительно имеет смысл, так это небольшой вариант, менее броский, но гораздо более верный: «Противоположность противоположности — это сама вещь».
Что противоположно «противоположности счастья»?
Ну, «противоположность счастливому» — это грустно.
Таким образом, противоположность и снова «счастлива».
Для сложения и вычитания с отрицательными значениями я предпочитаю долговую модель.
Для умножения и деления с отрицанием, я думаю, необходим немного более абстрактный подход — все дело в свойствах умножения.
Я считаю, что хорошие ментальные модели более эффективны, чем мантры типа «два негатива дают позитив». Но даже если бы это было не так — даже если бы использование мантр приводило к безошибочным вычислениям с отрицаниями — я бы все равно предпочел подход «ментальной модели». Изучение новых моделей порождает богатое мышление, которое должно быть на уроке математики; изучение новых мантр порождает некритическое мышление последователя культа.
Но даже если бы это было не так — даже если бы использование мантр приводило к безошибочным вычислениям с отрицаниями — я бы все равно предпочел подход «ментальной модели». Изучение новых моделей порождает богатое мышление, которое должно быть на уроке математики; изучение новых мантр порождает некритическое мышление последователя культа.
Нравится:
Нравится Загрузка…
Опубликовано
Математика с плохими рисунками на Facebook
Адрес электронной почты
Присоединяйтесь к 13 885 другим подписчикам
Архивы
Выберите месяц Май 2022 (1) Апрель 2022 (1) Март 2022 (3) Февраль 2022 (3) Январь 2022 (2) Октябрь 2021 (1) Сентябрь 2021 (3) Июль 2021 (4) Июнь 2021 (4) Май 2021 ( 8) апрель 2021 г. (2) март 2021 г. (1) январь 2021 г. (1) декабрь 2020 г. (3) июнь 2020 г. (2) май 2020 г. (1) апрель 2020 г. (3) март 2020 г. (3) февраль 2020 г. (4) январь 2020 г. ( 4) декабрь 2019 г.(5) ноябрь 2019 г. (7) октябрь 2019 г. (7) сентябрь 2019 г. (2) июль 2019 г. (1) июнь 2019 г. (3) май 2019 г. (2) апрель 2019 г. (3) март 2019 г. (4) февраль 2019 г. (5) январь 2019 г. (6) декабрь 2018 г. (1) ноябрь 2018 г. (3) октябрь 2018 г. (3) сентябрь 2018 г. (4) август 2018 г. (5) июль 2018 г. (3) июнь 2018 г. (4) май 2018 г. (2) март 2018 г. (2) февраль 2018 г. (5) январь 2018 г. (6) декабрь 2017 г. (4) ноябрь 2017 г. (5) октябрь 2017 г. (9) сентябрь 2017 г. (8) август 2017 г. (5) июль 2017 г. (4) июнь 2017 г. (4) май 2017 г. (5) апрель 2017 г. (4) март 2017 г. (5) февраль 2017 г. (4) январь 2017 г. (4) декабрь 2016 г. (4) ноябрь 2016 г. (5) октябрь 2016 г. (3) сентябрь 2016 г. (11) август 2016 г. (5) июль 2016 г. (4) июнь 2016 г. (4) май 2016 г. (4) апрель 2016 г. (4) март 2016 г. (5) февраль 2016 г.
(2) март 2021 г. (1) январь 2021 г. (1) декабрь 2020 г. (3) июнь 2020 г. (2) май 2020 г. (1) апрель 2020 г. (3) март 2020 г. (3) февраль 2020 г. (4) январь 2020 г. ( 4) декабрь 2019 г.(5) ноябрь 2019 г. (7) октябрь 2019 г. (7) сентябрь 2019 г. (2) июль 2019 г. (1) июнь 2019 г. (3) май 2019 г. (2) апрель 2019 г. (3) март 2019 г. (4) февраль 2019 г. (5) январь 2019 г. (6) декабрь 2018 г. (1) ноябрь 2018 г. (3) октябрь 2018 г. (3) сентябрь 2018 г. (4) август 2018 г. (5) июль 2018 г. (3) июнь 2018 г. (4) май 2018 г. (2) март 2018 г. (2) февраль 2018 г. (5) январь 2018 г. (6) декабрь 2017 г. (4) ноябрь 2017 г. (5) октябрь 2017 г. (9) сентябрь 2017 г. (8) август 2017 г. (5) июль 2017 г. (4) июнь 2017 г. (4) май 2017 г. (5) апрель 2017 г. (4) март 2017 г. (5) февраль 2017 г. (4) январь 2017 г. (4) декабрь 2016 г. (4) ноябрь 2016 г. (5) октябрь 2016 г. (3) сентябрь 2016 г. (11) август 2016 г. (5) июль 2016 г. (4) июнь 2016 г. (4) май 2016 г. (4) апрель 2016 г. (4) март 2016 г. (5) февраль 2016 г.


