Колыбель ньютона принцип действия: Колыбель Ньютона »

Колыбель Ньютона, исследовательская работа | Образовательная социальная сеть

Муниципальная научно – практическая конференция

« Фундаментальные и прикладные исследования в области естественно – математических наук»

Колыбель Ньютона

(направление физика)

Автор: Алферьева Ксения

МБОУ СОШ № 10 г. Апатиты, 9Б класс

Научный руководитель:

Титовская Светлана Николаевна

учитель, МБОУ СОШ № 10

Апатиты

2018

Содержание

1. Введение
2. Теоретическая часть

2.1. Маятники. Виды маятников.

2.2. История открытия маятника Ньютона

2.3. Принцип работы маятника Ньютона.

2.4. Применение маятника Ньютона.

3. Практическая часть

1. Изготовление маятника
2. Анализ результатов эксперимента

4. Заключение
5. Список литературы
6. Приложения

Слайд 1

Введение.

Очень часто дети думают, что физика – какая-то академическая наука, ученые ставят эксперименты в лабораториях, теоретики пишут теории, не выходя из кабинета. Может быть, так оно и есть. Но, все же, то, о чем они пишут теории и ставят эксперименты, происходит рядом с нами, да и в нас самих. Именно это нам пытаются донести  на уроках.  Физика – наука экспериментальная. Сейчас существует много способов заинтересовать учащихся изучать эту сложную и важную для жизни каждого человека науку: обучающие интернет сайты, научно — популярная литература и даже интерактивные музеи. Но именно на уроке физики, я узнала о законе сохранения импульса и энергии, о  различных маятниках и решила попробовать сделать один из них своими руками.

(Слайд 2) Цель работы: конструирование прибора – модели  маятника Ньютона.

Задачи:

1. Проанализировать литературу по рассматриваемому вопросу.
2. Продумать конструкцию маятника с наименьшими затратами и хорошим эстетическим видом.
3. Изготовить и привести в действие прибор — маятник Ньютона.
4. Узнать практическое применение «Колыбели Ньютона».

Гипотеза: Сконструированный маятник Ньютона продемонстрирует законы взаимосвязи механической энергии и импульса.

Актуальность выбранной темы обусловлена значением изучения законов сохранения энергии, они доказывают взаимосвязь явлений природы. Такие понятия, как «импульс», «работа», «энергия» в последующем необходимы для изучения многих физических  разделов. При изучении данной темы развиваются такие умения, как наблюдать, ставить эксперимент, конструировать, анализировать.

2. Теоретическая часть.

2.1.Маятники. Виды маятников.

(Слайд 3) Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.

Во время колебаний маятника происходят постоянные превращения энергии из одного вида в другой. Кинетическая энергия маятника превращается в потенциальную энергию (гравитационную, упругую) и обратно. Кроме того, постепенно происходит преобразование кинетической энергии в тепловую, за счёт сил трения.

Одним из простейших маятников является шарик, подвешенный на нити. Идеализацией этого случая является математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.

Если размерами массивного тела пренебречь нельзя, но всё ещё можно не учитывать упругих колебаний тела, то можно прийти к понятию физического маятника. 

Физический маятник — твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.

Система из нескольких шариков, подвешенных на нитях в одной плоскости, колеблющихся в этой плоскости и соударяющихся друг с другом, называется маятником Ньютона. Здесь уже приходится учитывать упругие процессы и законы сохранения импульса.

Ещё одним простейшим маятником является пружинный маятник. Пружинный маятник — это груз, подвешенный на пружине и способный колебаться вдоль вертикальной оси.

(Слайд 4) Маятник Фуко — это груз, подвешенный на нити, способный изменять плоскость своих колебаний.

(Слайд 5) Крутильный маятник — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью.

( Слайд 6) Маятник Капицы — пример динамически стабилизированного перевернутого маятника.

Маятники используются в различных приборах, например, в часах и сейсмографах.

Маятники облегчают изучение колебаний, так как наглядно демонстрируют их свойства.

2.2. История открытия маятника Ньютона.

(Слайд 7) Великий учёный Исаак Ньютон изобрел наглядную демонстрацию преобразования энергии — маятник или как ее еще называют — колыбель. Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь к прочному основанию П-образной формы.

Исследование и использование маятниковых устройств для демонстрации закона воздействия между несколькими телами, было сначала описано учёным Мариоттом в 17-м столетии.  Кроме Ньютона, принцип маятника использовали и другие физики. Среди них Христиан Гюйгенс, который изучал столкновение, а также физик Аббе Мэрайотт, он изучал закон воздействия тел друг на друга.   

Есть много разногласий, как же все-таки появилась современная колыбель Ньютона. К примеру, Мариуса Морина считают учёным, который первым сконструировал и дал название популярной сегодня конструкции. Он сделал для своей компании деревянную версию маятника. Сувениры — шары  были успешно проданы и положили начало рынку таких игрушек.

Продавать изобретение Исаака Ньютона в 1967 году предложил Саймон Преббл, актер из Англии. Именно он и дал название прибору — «колыбель Ньютона». С тех пор маятник стал популярным сувениром и прекрасной деталью в интерьере. 

(Слайд 8) Истории известен случай, когда сделали очень большое устройство маятника из 501 тонны бетона и листовой стали. Но это устройство колыбели за счет массивности имело погрешности в действии. Версия меньшего масштаба состояла из пяти 6-дюймовых хромовых шариков-подшипников стали, каждый из которых весил 33 фунта. Эта модель была практически такая же эффективная как настольная версия. В Соединённых Штатах Америки в Мичигане установили самую большую модель колыбели Ньютона. Она состоит из 16 шаров для боулинга, которые весят 6.8 кг каждый. Они крепятся на прочных тросах длиной 6.1 метра и возвышены на 1 метр над землей.  (приложение 1)

Устройство колыбели с самыми большими шарами столкновения диаметра на общественном дисплее, демонстрировалось больше года в Милуоки, Висконсин в американской Науке розничного магазина и Излишке. Каждый шар был надувным шаром осуществления 26 дюймов в диаметре (приложенный в клетке стальных колец) и был поддержан от потолка, используя чрезвычайно сильные магниты. Это было демонтировано в начале августа 2010 из-за проблем обслуживания.

2.3. Принцип работы маятника Ньютона

(Слайд 9) Если к шарикам не прикасаться, то они все время находятся в неподвижном состоянии. Чтобы увидеть движение маятника, нужно привести в действие крайний шар, тогда шар на другом краю будет совершать колебания с такой же скоростью и амплитудой, как и предыдущий. Движения происходят по конкретной траектории и с постоянной частотой.  Это демонстрирует закон сохранения импульса, а также превращение потенциальной энергии в кинетическую и наоборот.

Поскольку первое тело производит ударную волну, она передается через промежуточные сферы, которые остаются неподвижными, и воспроизводиться в последнем шаре. Если бы не было затрат энергии и препятствий таких как трение, маятник мог бы стать вечным двигателем. Но в природе это невозможно и колебания шаров со временем утихают, поскольку движению препятствуют диссипативные силы (силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту).  Энергетические потери – причина по которой шары в конечном счете останавливаются. Более высокий вес стали уменьшает относительный эффект сопротивления воздуха. Размер стальных шаров ограничен, потому что столкновения могут превысить упругий предел стали, исказив его и порождения тепловых потерь. Продолжительность работы маятника напрямую зависит от веса и размера шариков: чем больше их диаметр и чем они тяжелее, тем дольше будет длиться данный процесс, и наоборот.

Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд незаметно, как следующий шарик приминает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как: шарик немножко “вздрагивает”. Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое и ему некуда разогнаться, то он может на своем коротком пути передать импульс третьему шарику и в итоге остановиться.

Такое же действие совершает и следующий шарик, и так далее. Второе тело принимает импульс потенциальной энергии от предыдущего, но поскольку нет возможности превращения потенциальной энергии в кинетическую, то импульс передается от второго шара далее — в третий, четвертый, пятый. У последнего шарика некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определенную на высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.

Представим маятник, состоящий всего из двух сфер. В этом случае шар в движении сталкивается с соседом, который пребывает в состоянии покоя. Соприкасание упругое и центральное (так как оно наблюдается в идеальной колыбели Ньютона). Чтобы сосчитать скорости шаров после упругого столкновения, необходимо воспользоваться уравнением закона сохранения импульса для такой схемы и уравнением закона сохранения энергии, а потом развязать полученную систему уравнений. Итог известен: шар, который двигался останавливается, а тот, что пребывал в состоянии покоя, обретает скорость первого.  

Колебания похожи на распространение упругой волны в твёрдом теле, или же на посыл упругих возмущений и энергии упругой деформации без переноса вещества, как это происходит со звуком. Этот закон будет работать, если давать ускорение двум или трем телам одновременно.   

2.4. Применение маятника

(Слайд 10) Шары Ньютона признали еще в конце 20 века, они чаще всего применялись для релаксации, в психотерапии, а также для подсчета времени.  Декоративная модель шаров Ньютона пользуется неизменной популярностью уже многие годы. Мерное колебание, монотонное постукивание шаров и их блеск способствуют расслаблению. Это отличное средство для нервной системы, наблюдается несколько типов влияния:

— успокаивает нервы;

— снимает стрессс;

— помогает привести мысли в порядок;

— отвлекает от проблем;

— расслабляет;

— концентрирует внимание.

Многие приобретают ее для офиса, устанавливают в кабинете или на рабочем столе. Маятник спасает в ситуациях, когда в разгар трудового дня никак не получается сконцентрироваться на главном из-за больших умственных нагрузок. За движением шаров можно наблюдать бесконечно. Отзывы довольных обладателей доказали, что энергия от движения маятника преобразовывается в интенсивный поток мыслей, интересных идей и в замечательное настроение на целый день.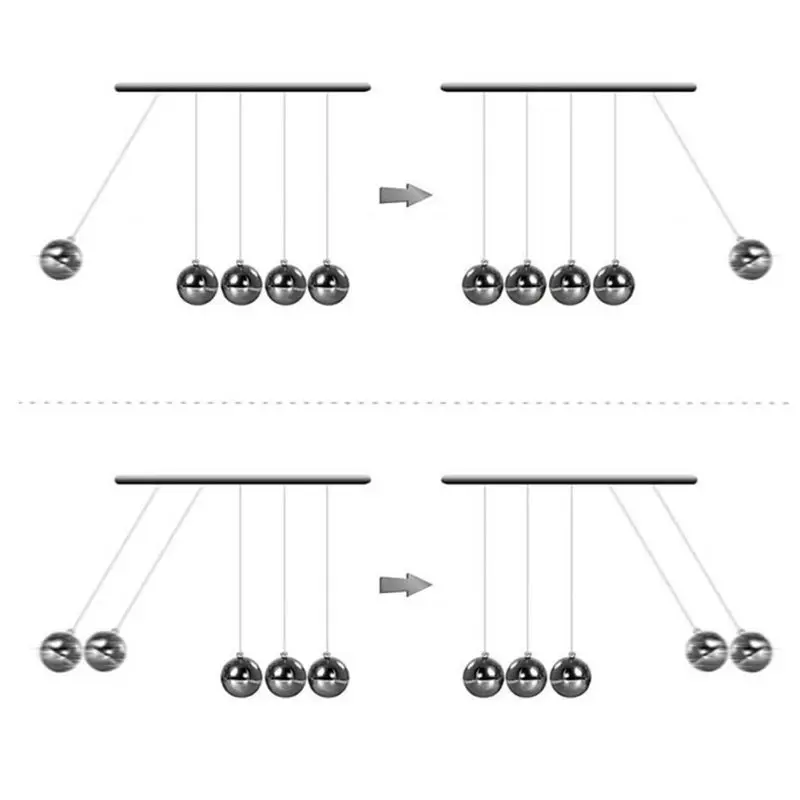   

Удовольствие аксессуар приносит также из-за того, что вы смотрите и знаете, что это инсталляция закона сохранения импульса и сохранения энергии, поэтому наблюдение плавного движения шаров имеет особый смысл. Маятник станет отличной деталью интерьера кабинета в стиле хай-тек, это оригинально и стильно. Маятник Ньютона — прекрасный подарок для человека, который увлекается, разними диковинками, головоломками и конструкторами. 

Колыбель Ньютона как средство против раковых опухолей

(Слайд 11) Исследователи из Калифорнийского технологического института (Cal Tech), используя модифицированный принцип колыбели Ньютона, добились эффекта концентрации и усиления звуковых волн, наделяя их, таким образом, чрезвычайной разрушительной силой. Используя в качестве основы акустическую линзу из метаматериалов, ученые расположили в ряд 21 металлический шарик. Звуковая волна, возникшая в результате удара по последнему шарику, двигаясь, постоянно усиливалась звуковой линзой и складывалась с новыми звуковыми волнами, возникшими от ударов шариков друг об друга, усиливаясь еще больше.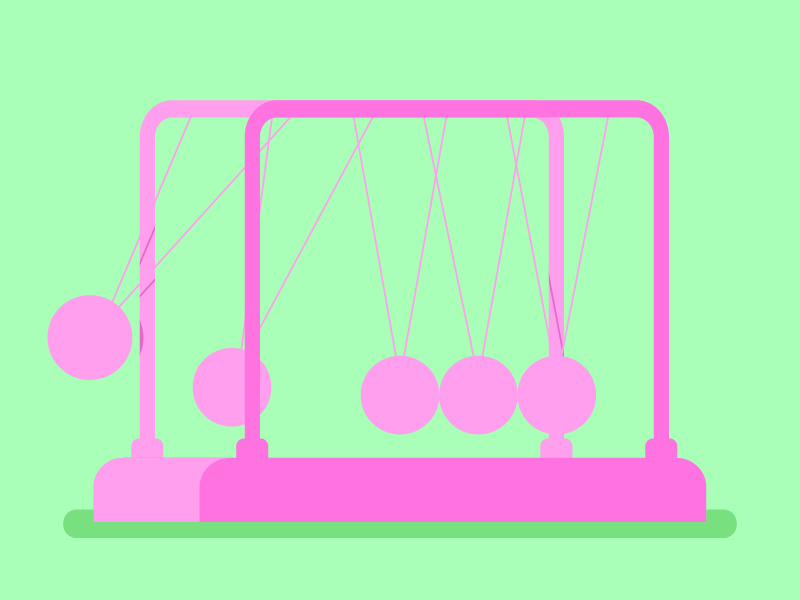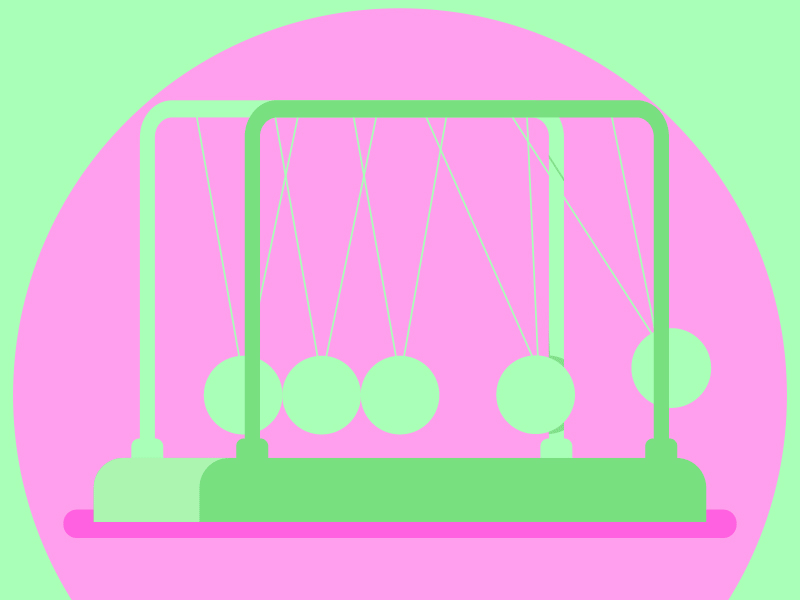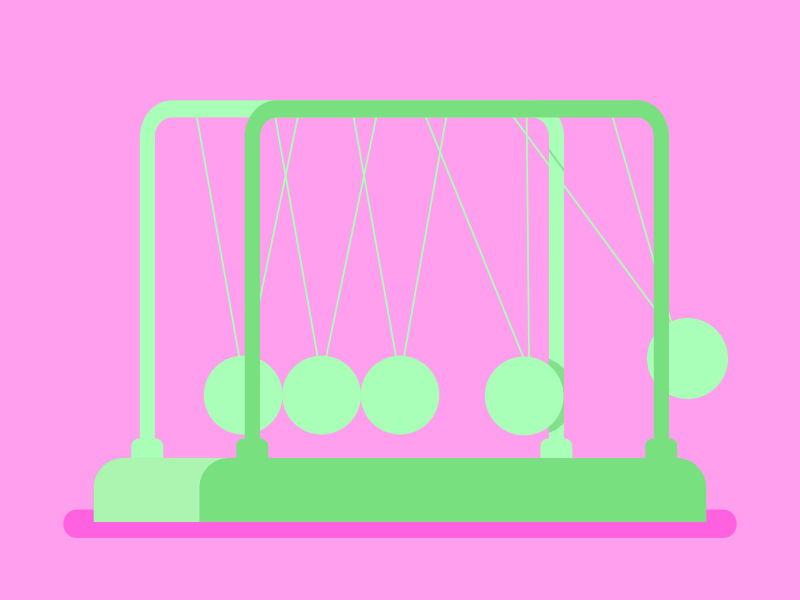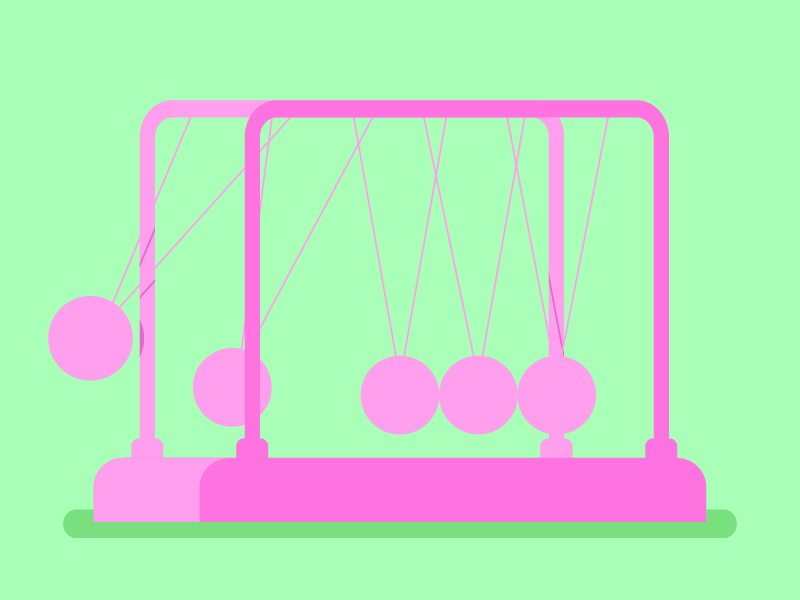 Но, в отличие от колыбели Ньютона, кинетическая энергия последнего шарика и созданная суммарная звуковая волна воздействовали на препятствие, изготовленного из метаматериала акустической линзы, с помощью которой вся энергия на выходе фокусировалась в очень маленьком объеме, создавая в нем звук невероятной мощности.

Поскольку «звуковые» пули, в отличие от обычных пуль, могут практически беспрепятственно проходить через воздух, воду и землю, их разрушительную энергию можно использовать для нанесения повреждений подводным лодкам, находящимся в погруженном состоянии, и для разрушения подземных укрытий. Но, с более мирной точки зрения, такая технология, в меньшем масштабе, может быть использована в медицинской области для «звуковой» рентгенографии. Так же «звуковые» пули могут быть использованы для разрушения клеток раковых опухолей, что позволит обойтись в некоторых случаях без хирургического вмешательства.

3. Практическая часть

(Слайд 12) 3.1. Изготовление маятника

Проанализировав литературу, я выделила требования при конструировании, изготовлении и применении самодельного прибора:

• четко представлять его назначение  и применение;

• заранее рассчитать его отдельные элементы, сделать необходимые схемы, чертежи;
• хорошо представлять принцип действия прибора;
• уяснить, на использовании каких законов основана его работа;
• от каких факторов зависит эффективность его демонстрации.

Для изготовления маятника Ньютона мне понадобилось: (приложение 2)

1. металлические бусинки (4 штук)
2. провод стальной (4 штук по 4 см)
3. клей «Момент»
4. линейка деревянная
5. картон

Ход работы:

1. Выбрать подставку для маятника
2. Рассчитать диаметр одного шарика.

Для того, чтобы шарики касались друг друга, необходимо вычислить их диаметр. Для расчета можно воспользоваться способом рядов:

3. На линейке сделать метки, соответствующие размеру одного шарика
4. Прикрепить бусинки к стальной проволоке с помощью плоскогубцев и клея
5. Закрепить стальную проволоку  и отрегулировать длину так, чтобы шарики касались друг друга.
6. Провести эксперимент.

2.  Анализ результатов эксперимента

В ходе конструированиямодели маятника и демонстрации эксперимента возник ряд трудностей:

1. Из стальной проволоки тяжело было сделать абсолютно круглое отверстие, для закрепления на конструкции.
2. Опора для маятника должна быть жесткой, даже маленькие шарики приводят к ее деформации, неустойчивости.
3. Колебания резко затухают, так как сложно выставить шарики в одну линию.

Несмотря на трудности, маятник Ньютона продемонстрировал передачу импульса и энергии от одного крайнего шарика к другому.

4. Заключение

Наблюдать за опытами, которые проводит учитель интересно, но проводить их самой интересно вдвойне, тем более, если сконструировала и сделала прибор своими руками.

В ходе данной работы я познакомилась с новыми физическими понятиями и величинами, такими как энергия, импульс и др. Убедилась, что способы, изученные на уроках физики, например способ измерения размеров малых тел ( способ рядов), может понадобиться для вычисления не только физических задач.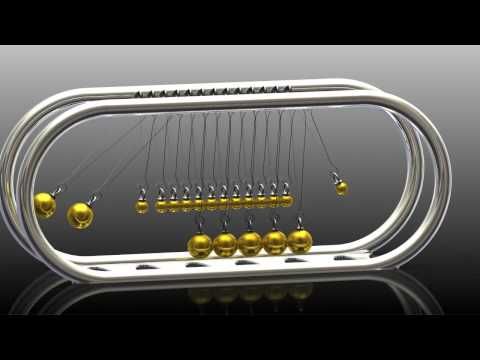

Маятник Ньютона, сконструированный мной, имеет некоторые технические недостатки и не смог длительное время совершать колебания, но выводы, сделанные в ходе эксперимента, могут позволить их исправить или минимизировать.

Данный маятник можно демонстрировать на уроках физики при изучении таких физических разделов, как «Механические колебания», «Законы сохранения в механике».

(Слайд 13)

Интернет ресурсы:

• https://ru.wikipedia.org/

• https://img.gazeta.ru/files3/882/3347882/soundbullm.jpg
• http://vitanar.narod.ru/revolucio/revolucio4/revolucio4.htm

(Слайд 14)  «Спасибо за внимание»

Приложение 1

Самая большая модель «колыбели Ньютона».

Маятник Ньютона — frwiki.wiki

Маятник Ньютона является маятником является пять шаром компонентов и для иллюстрации сохранения теорий импульса и энергии .

Анимация ньютоновского маятника.

Резюме

• 1 Описание
• 2 Впечатления
• 3 Консервативная интерпретация
  • 3. 1 Случай, когда мяч брошен
  • 3.2 Случай, когда бросают два мяча
  • 3.3 Случай, когда бросают три или более мячей
• 4 История и эпонимия
• 5 См. Также
  • 5.1 Связанная статья
  • 5.2 Внешние ссылки

Описание

Маятник Ньютона состоит из пяти металлических шаров одинаковой массы, подвешенных на двух проволоках к двум жестким стержням. Эти пять мячей касаются друг друга в состоянии покоя и расположены в средней плоскости двух стержней. Его действие основано на принципе ответных действий. Первый закон Ньютона гласит, что действует принцип действие-противодействие.

Опыт

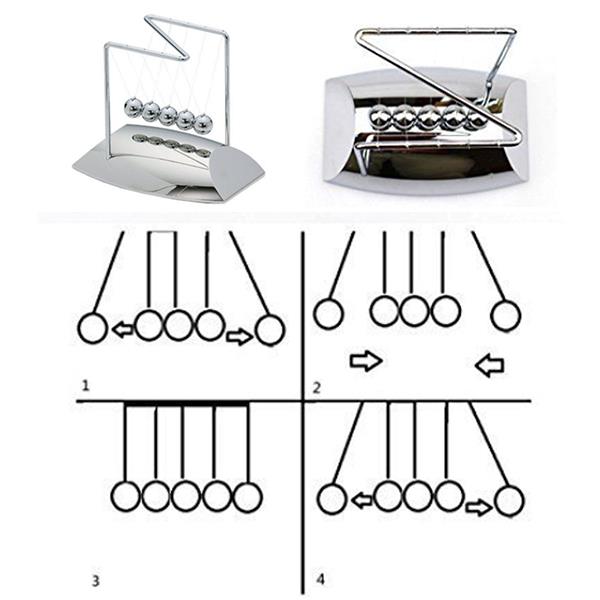
Варианты движения маятника Ньютона.

Когда вы бросаете два мяча, два шара с другой стороны начинают двигаться. При броске трех мячей с другой стороны два оставшихся шара приводятся в движение, когда мяч попадает в них. То же самое и с четырьмя шарами.

Менее известные опыты: если мы бросаем мяч в обе стороны одновременно, они отскакивают одновременно, в то время как трое в середине остаются неподвижными. Аналогично, с двумя шарами с каждой стороны, последний шар неподвижен. Если мы бросим три шара в одну сторону и два — в другую, они столкнутся и полетят три в одном направлении, два — в другом, поочередно.

Удаление неподвижного мяча, когда другой совершает движение в другую сторону, изменяет движение мяча.

Можно бросать несколько мячей в разное время, чтобы увеличить количество движений и ударов, но результаты часто искажаются из-за внешних воздействий и несовершенства материала.

Консервативная интерпретация

Принцип маятника основан на двух принципах сохранения, которые касаются соответственно кинетической энергии и количества движения.

Случай, когда мы бросаем мяч

Интерпретация здесь проще, если рассмотреть маятник только с двумя шарами. В этом анализе вызванные принципы сохранения приводят к системе двух уравнений, в которых характеристики маятника до и после столкновения шаров связаны. При исходных данных о шарах, которые представляют собой нулевую начальную скорость одного из них и равенство их масс, разрешение системы позволяет найти соответствующую скорость двух шаров после их столкновения. Затем было замечено, что эффект удара просто заключается в изменении скорости двух шаров.

Если мяч брошен с одной стороны на несколько других неподвижных, этот мяч останавливается после удара, а мяч, находящийся на другом конце, поднимается, восстанавливая движение первоначально брошенного шара.

Случай, когда мы бросаем два мяча

Два шара на противоположном конце поднимаются, потому что они поражены двумя ударами, временно отделенными от короткого промежутка времени .

При броске трех и более мячей

Для математической обработки столкновения «цепочки», состоящей более чем из 2 шаров, законов сохранения количества движения и кинетической энергии уже недостаточно. Предположим, есть 5 шариков; при известных начальных условиях необходимо 5 уравнений для определения 5 конечных скоростей.

Действительно, чтобы объяснить поведение цепи с более чем двумя шариками, необходимо принять во внимание определенное свойство устройства: мы рассматриваем «цепь» как систему, состоящую из масс и пружин (как мы это делаем с колебания кристаллической решетки). В этой системе распространяется волна. Только в том случае, если это распространение происходит без дисперсии, возникает поведение, наблюдаемое с шарами. Если пружины подчиняются закону Гука , мы получаем сильную дисперсию, и эксперимент не продолжается, как мы наблюдаем с шарами. Это легко показать на рельсе на воздушной подушке. Система, например, из 5 кареток плюс пружины в качестве упоров не ведет себя как шары. Когда вы бросаете две тележки против трех других, которые находятся в состоянии покоя, получается довольно хаотичное движение. Неразрывность цепочки шаров проистекает из того факта, что эквивалентные пружины, которые соответствуют давлению одной сферы на другую, вовсе не относятся к типу закона Гука.

История и эпонимия

Джон Уоллис , Кристофер Рен и Кристиан Гюйгенс представили Королевскому обществу в 1662 году мемуары, описывающие принципы работы этого маятника. Следовательно, Ньютон не участвовал в этом. У Рене Декарта была идея сохранения углового момента , но его решение проблемы не было полным.

Смотрите также

Связанная статья

• Маятник

Внешние ссылки

• Описание уравнений, связанных с маятником Ньютона
• (ru) Крис Шульц, «  Как работают колыбели Ньютона  » — Вводный текст.

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Что на самом деле произойдет, если вы бросите мяч в колыбель Ньютона?

Итак, следующий очевидный вопрос: сохраняется ли кинетическая энергия, как сохраняется импульс? Ответ: иногда. Для некоторых столкновений, которые мы называем «упругими столкновениями», сохраняются как кинетическая энергия, так и импульс. Как правило, упругие столкновения происходят между очень упругими объектами, например, между двумя резиновыми мячами или шарами для бильярда.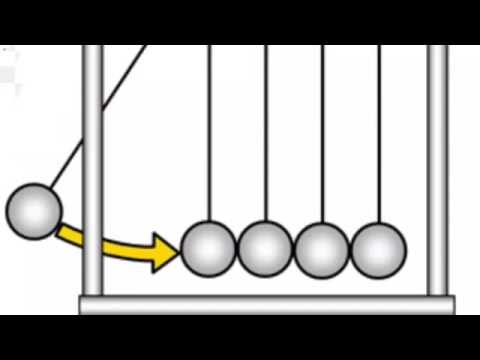 Если у нас есть упругое столкновение в одном измерении (что означает, что все происходит по прямой линии), то у нас есть два уравнения, которые мы можем использовать: сохранение импульса и сохранение кинетической энергии.

Кроме упругих столкновений есть еще два вида. Когда два объекта сталкиваются и слипаются, как кусок глины, ударяющийся о блок, мы называем это полностью «неупругим» столкновением. В этом случае импульс все еще сохраняется, и мы также знаем, что конечная скорость двух объектов одинакова, потому что они слипаются.

Наконец, есть случай, когда два объекта сталкиваются, но не слипаются. и не сохраняют кинетическую энергию. Мы просто называем их «столкновениями», поскольку они не являются одним из двух особых случаев (упругого и неупругого). Но помните, что во всех этих случаях импульс сохраняется до тех пор, пока столкновение происходит за короткий промежуток времени.

Хорошо, теперь давайте рассмотрим задачу, которая во многом является частью колыбели Ньютона.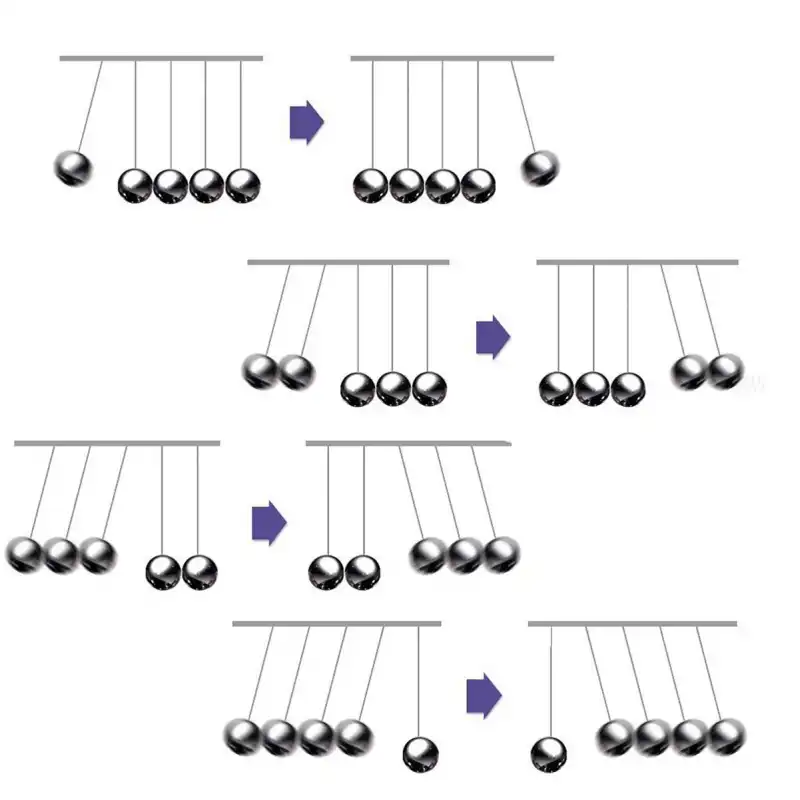 Предположим, у меня есть два металлических шара с одинаковой массой (m), шар A и шар B. Шар B стартует с места, а шар A движется к нему с некоторой скоростью. (Назовем это v ₁ .)

До столкновения полный импульс был бы mv ₁ + m×0 = mv ₁ (поскольку мяч B стартует с места). После столкновения полный импульс должен быть равен mv ₁ . Это означает, что оба шара могли двигаться со скоростью 0,5v ₁ или какая-то другая комбинация, если общий импульс равен mv ₁ .

Но есть еще одно ограничение. Так как это упругое столкновение, кинетическая энергия должна сохраняться и . Вы можете посчитать (это не слишком сложно), но оказывается, что для сохранения как KE, так и импульса есть только два возможных исхода. Первая состоит в том, что мяч А достигает скорости v ₁ , а мяч В остается неподвижным. Это именно то, что произошло бы, если бы мяч А пролетел мимо мяча В. Другой возможный результат состоит в том, что мяч А останавливается, и тогда мяч В имеет скорость v ₁ . Возможно, вы видели, как это происходит, когда бильярдный шар сталкивается с неподвижным шаром лоб в лоб. Движущийся шар останавливается, а другой шар движется.

Примерно так и происходит с колыбелью Ньютона. Если столкновения между шарами упругие (это справедливое приближение) и все выровнено (так что это одномерно), то единственное решение для шара с одной стороны, ударяющего стопку, состоит в том, чтобы он остановился, а другой шар начал двигаться. вместо. Это единственный способ сохранить и кинетическую энергию, и импульс. Если вы хотите узнать все подробности об этом выводе, вот вам видео:

Как насчет неупругого столкновения? Это довольно легко. Поскольку оба шара имеют одинаковую массу и одинаковую скорость (поскольку они слипаются), единственное решение состоит в том, чтобы они оба после столкновения двигались со скоростью 0,5v ₁ . В случае простого столкновения (ни упругого, ни неупругого) оба шара будут иметь скорость от 0 до v ₁ .

В качестве демонстрации вот три сталкивающихся шара. Вверху показано упругое столкновение, внизу — неупругое, а в середине — что-то среднее.

Видео: Ретт Аллен

Мне кажется, это просто круто.

Видеоанализ сверхбыстрой колыбели

Есть несколько вещей, которые отличают столкновение из видео Slow Mo Guys от действия обычной колыбели Ньютона. Вместо пяти шаров в сетапе есть шестой, который вылетает из воздушной пушки. Этот шар движется очень быстро, но он также выглядит немного меньше, чем другие шары в люльке, а это значит, что у него другая масса.

И, как вы можете видеть на видео, вместо того, чтобы шар в конце колонны просто отскакивал наружу, четыре из пяти шаров полностью отрываются от своих нитей и улетают, когда основание падает. Это не будет работать как хорошая щелкающая офисная игрушка (и она может проделать дыру в вашей стене).

Как работает колыбель Ньютона? • Загадочное творение

В колыбели Ньютона, когда шар с одной стороны ударяется о последующие неподвижные шары, шар на конце отталкивается наружу. Как это возможно?

Колыбель Ньютона, также известная как шары Ньютона, представляет собой образовательный инструмент, работающий на основе законов сохранения энергии и импульса. С одной стороны, колыбель Ньютона снимает стресс и находится на столе каждого успешного человека, а с другой стороны, для многих она является привлекательным развлечением.

Колыбель Ньютона была названа в 1967 году английским актером Саймоном Пребблом в честь Исаака Ньютона. Это устройство также известно как качалка Ньютона, шары Ньютона и маятник Ньютона.

История колыбели Ньютона

Несмотря на свое название, теоретические принципы колыбели Ньютона были представлены в документах Королевскому обществу в 1962 году Джоном Уоллисом, Христианом Гюйгенсом и Кристофером Реном. В частности, именно Гюйгенс отметил сохранение кинетической энергии и количества движения. Поскольку термин «кинетическая энергия» не вводился почти столетие, Гюйгенс называл лежащий в его основе принцип величиной, пропорциональной квадрату массовой скорости.

Рене Декарт, французский философ, предложил идею сохранения, но не смог полностью решить проблему. Согласно этому философу,

Импульс = Масса x Скорость

Это работает только в некоторых ситуациях, но не при столкновениях между объектами.

Позже Гюйгенс предложил изменение, которое решило проблему. Гюйгенс предложил заменить скорость на скорость, потому что скорость подразумевает направление движения, поэтому импульс двух тел одинакового размера, движущихся с одинаковой скоростью в противоположных направлениях, будет равен нулю.

Почему имя Ньютона получило признание?

Ньютон получил признание в основном по двум причинам:

1. Второй закон движения Ньютона выводит закон сохранения импульса. Интересно, что Ньютон опубликовал свои законы движения в 1687 году, через двадцать пять лет после того, как Гюйгенс открыл закон сохранения импульса.
2. Ньютон был более известен, чем Гюйгенс, и его общее влияние на мир физики было намного больше, чем кто-либо другой.

Конструкция колыбели Ньютона

Существует несколько художественных модификаций колыбели Ньютона, но базовая установка состоит из нескольких шаров, подвешенных в линию с двух перекладин параллельно линии шаров. Для устойчивости поперечины крепятся к тяжелому основанию. Шарики подвешены на светлых проволоках, образуя перевернутый треугольник.

Все шары одного размера и имеют одинаковый вес, массу и плотность.

Мячи могут быть любого размера, веса и массы при условии, что все они имеют одинаковый размер, вес и массу. Не менее важно выравнивание мячей по отношению к перекладинам. Хотя подойдет любое количество шаров, обычно это нечетное количество шаров.

Из чего сделаны эти мячи?

Шарики изготовлены из материала с высокой эластичностью и равномерной плотностью. Как известно, материал с высокой эластичностью больше отскакивает, следовательно, высокая эластичность материала позволяет шарикам двигаться более длительное время.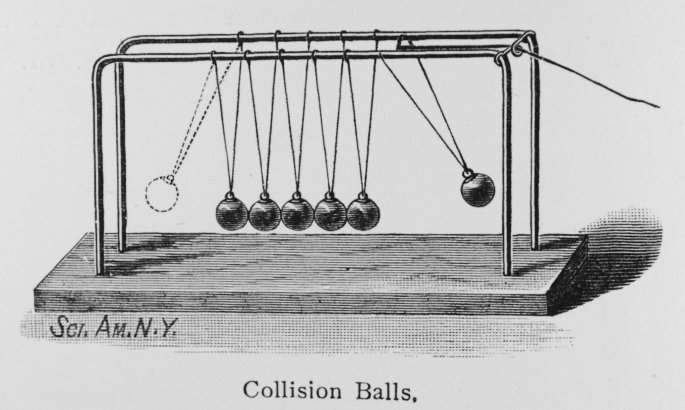 Обычно для люльки Ньютона используется нержавеющая сталь. Титан тоже можно использовать, но он дорогой.

Нержавеющая сталь не деформируется, а сжимается на несколько микрон при ударе о следующий шар.

Одинаковая плотность шаров обеспечивает передачу энергии между шарами без особых помех.

Новый вид высокоэластичного сплава, используемого для изготовления колыбели Ньютона, представляет собой аморфный металл. Но поскольку они дороги в производстве, в настоящее время они не используются. У них нет готовых точек сдвига, поскольку расплавленный металл быстро охлаждается для получения случайного молекулярного выравнивания, в отличие от обычных металлов, которые имеют кристаллоподобное выравнивание.

Принцип работы колыбели Ньютона

Как упоминалось ранее, эта колыбель работает на основе законов сохранения энергии и импульса.

Закон сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена, а преобразована из одной формы в другую. Закон сохранения импульса гласит, что при столкновении двух объектов в изолированной системе импульс остается одним и тем же, то есть сохраняется до и после столкновения.

В покое, 

• Высота, h = 0
• v = 0
• Потенциальная энергия = mgh = 0 
• Кинетическая энергия = (1/2)mv2 = 0
• Импульс = mv = 0

Когда первый шар поднимается, высота 980068 90 увеличивается

Когда мяч отпускается,

• Высота уменьшается
• Потенциальная энергия преобразуется в кинетическую энергию
• Мяч приобретает импульс

В нижней части качелей,

• Вся потенциальная энергия преобразуется в кинетическую энергию
• Мяч достигает максимальной скорости

Удар по следующему мячу, первый мяч полностью теряет свою энергию

Передает энергию и импульс следующему мячу, по которому он ударяется.

Процесс компрессии и декомпрессии продолжается до последнего шарика.

Последняя сфера

• Распаковывается.
• Нет передачи энергии, так как нет последующего шара.
• Без потерь энергии
• Взлетает вверх со скоростью, равной выпущенной скорости первого мяча, с сохранением импульса
• Высота подъема последнего мяча = высоте падения первого мяча.

Что если выпустить более одного мяча?

Поскольку мы знаем, что каждый шар передает достаточно энергии, чтобы сдвинуть с места другой шар, количество шаров, подброшенных в воздух, будет равно количеству выпущенных шаров. Кроме того, мы знаем, что

Импульс = Масса X Скорость

Чтобы сохранить импульс, если массы шаров равны, скорость также останется неизменной.