Тест шесть квадратов: Познай себя: Психологический тест 6 квадратов

Тест Вартегга

2. Главная
3. Диагностика
4. Тест Вартегга

Внимание. Ради сохранения психического здоровья Ваших детей результаты теста может интерпретировать только опытный психолог!

Данный тест направлен на исследование многих факторов: самооценки, социальных навыков; амбиций, активности и способов достижения цели; внутренней устойчивости; особенностей личностных взаимоотношений; отношение к страхам.

Автор теста – немецкий психолог Эрик Вартегг. Тест был опубликован в 1963г, в России появился в 2004г благодаря В.К. Калиненко в его книге «Рисуночный тест Вартегга».

Сам тест представляет собой лист А4, поделенный толстыми черными линиями на 8 равных квадратов. В каждом квадрате содержится строго определенный рисунок, который нужно продолжить. Вы можете самостоятельно сделать бланк для теста, распечатав эту таблицу в формате А4.

Задание: продолжите рисунок в каждом квадрате так, чтобы в нем получился законченный рисунок. Вы можете заполнять квадраты в любой последовательности и использовать различные цвета. Затем подпишите рисунки.

Интерпретация теста Вартегга

При интерпретации теста Вартегга учитываются следующие показатели:

— смысловое содержание рисунка,

— особенности графики (нажим, штриховка, расположение),

— порядок заполнения квадратов.

Стимульный рисунок в каждом квадрате активизирует определенный аспект личности, то есть является бессознательным символом для определенной части психики. Все эти «черточки и точечки» не случайны, а являются результатом работы многих великих психологов: К. Юнга и его последователей, которые изучали коллективное бессознательное.

Квадраты № 1, 2, 7 и 8 – это эмоциональные реакции, мир чувств. Обычно здесь располагается живое: природа, люди, животные.

Квадраты № 3, 4, 5 и 6 – это рациональные реакции, мир логики. Обычно здесь располагаются неодушевленные предметы, созданные человеком.

Если вы заметили отклонение от этого правила – ищите в этом квадрате (теме) проблему.

Квадрат №1: символически точка означает начало, а в данном случае – самого себя, то есть представление о себе и свое место в мире.

Квадрат №2: волнистая линия – это зародыш, а пространство вокруг – мир людей. Таким образом, этот квадрат показывает характер взаимоотношений с окружающими.

Квадрат №3: три восходящие линии символизируют рост и развитие. В данном случае они отражают мотивацию, планы на будущее, амбициозность.

class=»eliadunit»>

Квадрат №4: черный квадрат – это символ опасности, страха, вины. Этот квадрат покажет отношение к жизненным препятствиям, опасностям, трудностям, психологическому грузу, который несет человек.

Квадрат №5: две перпендикулярные линии означают сопротивление, препятствие на пути. По этому рисунку можно увидеть, как человек справляется с трудностями, преобладает ли стратегия достижения успеха или избегания неудач. Предполагается, что рисунок будет направлен вправо вверх.

Квадрат №6: две линии означают противоположные начала, идущие в разных направлениях, но требующие пересечения. В данном случае это отношения с близкими людьми: сближение или отдаление от них. Предполагается, что линии будут соединены в рамку или другую целостность.

Квадрат №7: точки символизируют чувствительность, интуицию, восприимчивость к внешним и внутренним раздражителям. Этот рисунок отражает чувствительность, тактичность, ранимость или, наоборот, «толстокожесть».

Квадрат №8: дуга – символ гармонии и защиты. В рисунке означает чувство удовлетворенности, защищенности, источник сил. Закрытые предметы – уход в себя в качестве защиты.

Особенности графики:

Чтобы оценить нажим, нужно перевернуть рисунок. Тогда с изнаночной стороны будут хорошо видны области сильного и совсем слабого нажима: именно эти вопросы (квадраты) вызывают наибольшее напряжение у рисующего, то есть являются проблемными, трудными, однако указывают на его решимость и боевой настрой! Слишком слабый нажим может указывать на неуверенность, слабость, подавленность в этом аспекте (квадрате).

Расположение рисунка в верхней части квадрата указывает на излишнюю самоуверенность, преувеличение своих возможностей, в нижней части – на неуверенность и преуменьшение способностей, сбоку – зависимость и поиск поддержки, в центре – адекватную самооценку и уверенность в себе.

Преобладающие линии: горизонтальные – слабость, вертикальные – решительность, штриховка – тревожность.

Размер рисунка: сверхбольшие – демонстративность, бурная эмоциональность, совсем маленькие – подавленность, скромность.

Отношение к исходным данным: «линии и точки»:

Ребенок игнорирует их, то есть рисунок исследуемого не связан с ними – сосредоточен на себе, своем «Я», погруженность в «свой мир»;

Ребенок учитывает их в своем рисунке, но не полностью – изобретательность;

Учитывает все – концентрация на конкретном, важном, существенном;

Создает целостные интересные образы – творческие способности.

Порядок заполнения квадратов: ребенок обычно начинает с тех квадратов, которые ему «нравятся», «легкие», «понятные», то есть из тех тем, которые для него наиболее актуальны, важны. А квадраты, которые «не нравятся», «какие-то непонятные», «сложные», оставляет на потом, то есть те темы, в которых он испытывает затруднения.

Пример интерпретации данного рисунка с тестом Вартегга можно скачать ниже.

Мы в соцсетях

Популярные материалы

• Главная

• Открытое занятие психолога (сказкотерапия) в старшей группе: «Развитие базовых эмоций и воли»

• Открытое занятие психолога с элементами сказкотерапии в подготовительной группе: «Сказочное путешествие»

• Тренинг для родителей «Когда в семье «тяжелые» родители»

• Коррекционно-развивающая программа для развития познавательных процессов дошкольников 4 года жизни «Подари добро»

• Программа развития интеллекта детей 6-7 лет

Как проводить и оценивать тест “Конструктивный рисунок человека”

В этой статье мы рассмотрим проективный тест “конструктивный рисунок человека” и расскажем, как интерпретировать его результаты.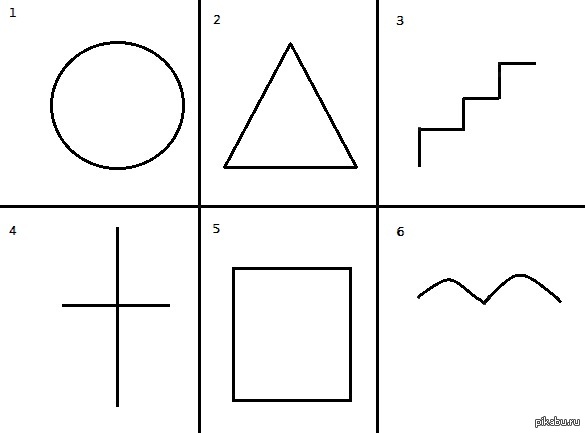

Определение психотипа человека – одна из задач HR-специалиста. Рисуночные проективные тесты – ценный инструмент, позволяющий выявить и оценить личностные качества сотрудника.

Что такое проективные тесты

Цель проективных тестов состоит в том, чтобы узнать личностные характеристики человека, выявить эмоциональные и внутренние конфликты, в случае необходимости дать совет и помочь. Посредством интерпретации ответов HR-менеджер может выявить те эмоции, желания и конфликты, могут негативно сказаться на работе и эмоциональном состоянии сотрудников.

Использование проективных методик широко распространено, как при приеме на работу, так и при принятии решения о повышении сотрудников внутри компании.

Как проводить тест

Задача методики: изучить индивидуально-типологические различия сотрудников.

Инструменты: три листа бумаги, карандаш, ручка. Каждый лист бумаги нумеруется.

Инструкция: сотрудники, проходящие тест, получают три листа бумаги. На каждом и них они должны изобразить фигуру человека, состоящую из 10 геометрических фигур. Использовать можно только квадрат, круг и треугольник.

Обратите внимание, должно получиться три рисунка, по одному на каждом из листов. Последующий анализ результатов включает в себя все три изображения. Можно менять размер элементов и накладывать их друг на друга. Важно использовать все три типа фигур в каждом рисунке.

Обработка результатов

Обработка, полученных данных, осуществляется следующим образом: на каждом из рисунков подсчитывается количество нарисованных геометрических фигур определенного типа (кругов, квадратов, треугольников).

Результат записывается в виде трехзначных чисел где:      

• треугольники обозначают сотни   
• круги – десятки  
• квадраты – единицы

Полученные цифры называют формулой рисунка, по которой осуществляется соотнесение испытуемых к определенным типам личности.

Основанная на предпочтении той или иной фигуры техника, формирует систему индивидуально-типологических различий, определяемых числовой комбинацией.

Типы личности по тесту

Организатор

Формулы рисунков: 604, 730, 721, 712, 811, 802, 910, 901, 640, 631, 622, 613, 703, 820.

Люди, чья формула рисунка попадает под данный психотип, имеют склонность к руководству, командованию, поучению. Они обладают высокими организационными способностями, умеют грамотно излагать информацию, убеждать. Организаторы хорошо адаптируются к социальной среде. Такие люди становятся хорошими лидерами и успешно справляются на руководящих должностях. Умеют управлять, организовывать и мотивировать большое количество сотрудников.

Старательный работник

Формулы рисунков: 550, 505, 532, 514, 541, 523.

Люди данного психотипа имеют склонность к руководству, но с трудом принимают ответственные решения. Отличаются высоким профессионализмом и ответственностью. Они болезненно реагируют на ложь, требовательны как к другим, так и к себе. Для таких сотрудников умение хорошо выполнять свою работу является очень важным.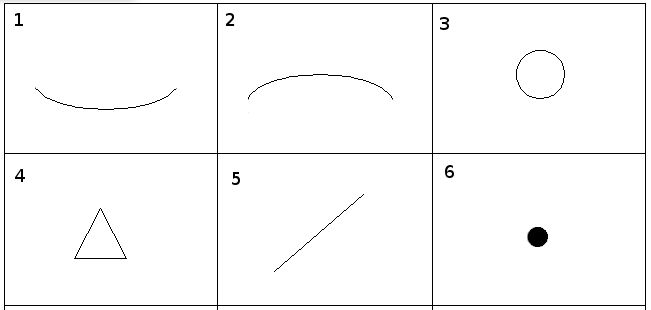 Они стремятся в совершенстве овладеть специальностью, поэтому, как правило, являются отличными профессионалами.

Инициатор

Формулы рисунков: 433, 424, 415, 406, 460, 451, 442.

Обладатели данного психотипа имеют разносторонние способности и таланты. Легко могут сменить сферу деятельности. Способны хобби превратить в дополнительный источник дохода. Педантичны, не переносит беспорядка. Эти люди часто сомневаются в себе и своих способностях, поэтому нуждаются в одобрении и похвале.

Коммуникативный

Формулы рисунков: 415, 325, 235.

Такие люди относятся к большинству событий с легким юмором. Поэтому они легко выходят из конфликтных ситуаций и отлично находят общий язык практически со всеми. Как правило, имеют склонность к экономической деятельности.

Интуитивный

Формулы рисунков: 280, 262, 244, 217, 208, 226, 271, 325.

Люди данного типа альтруисты, любят проявлять заботу, обладают чувствительной

нервной системой, хорошо работают, переключаясь с одной деятельности на другую,

быстро утомляются, обладают отличными прикладными навыками. Помимо этого, им сложно на что-то решиться из-за того, что они долго анализируют информацию.

Независимый

Формулы рисунков:, 145, 136, 127, 118, 109, 046, 037, 028, 019.

Люди данного психотипа обладают отличными способностями, имеют богатое воображение. Чаще всего находят себя в искусстве или интеллектуальных профессиях. Способны самостоятельно принимать решения и брать на себя ответственность. Однако им трудно мириться с критикой и ограничениями.

Эмотивный

Формулы рисунков: 073, 064, 460, 451, 055, 190, 370, 361, 550, 091, 172, 163, 154, 262, 181, 253, 352, 082, 280, 271.

Такие люди склонны к сопереживанию, заботе о других, много тратят энергии на окружающих, поэтому тяжело находят себя в профессии. Затрудняются в раскрытии собственных способностей, самореализации. Эмотивные люди хотят изучать многие сферы, но достигают успеха, если сосредотачиваются на чем-нибудь одном.

Самодостаточный

Формулы рисунков: 505, 109, 208, 604, 703, 802, 901, 307, 406.

Самодостаточный психотип является противоположным эмотивному. Как правило, такой человек избегает близкого общения с теми, кто не умеет сдерживать эмоции. Если он профессионал своего дела, то может заставить других выполнять то, что нужно, проявляет давление на других. Люди, относящиеся к этому типу, не склонны делиться переживаниями, скорее они замыкаются в себе со своими проблемами.

Зачем проективные тесты нужны HR-менеджерам

Для того чтобы лучше понимать кандидатов и коллег, HR-менеджеры проводят разнообразные тестирования. Этот тест «Конструктивный рисунок человека» не исключение и он может иметь решающее значение в принятии решения о выборе нового сотрудника или повышения кого-либо на руководящую должность. На основании особенностей психотипа легче оценивать соответствие ролей в компании, принимать важные решения и предугадывать возможные конфликтные ситуации.

Самое важное в тесте – это правильная интерпретация результатов. Поэтому подойти к этому следует ответственно и внимательно.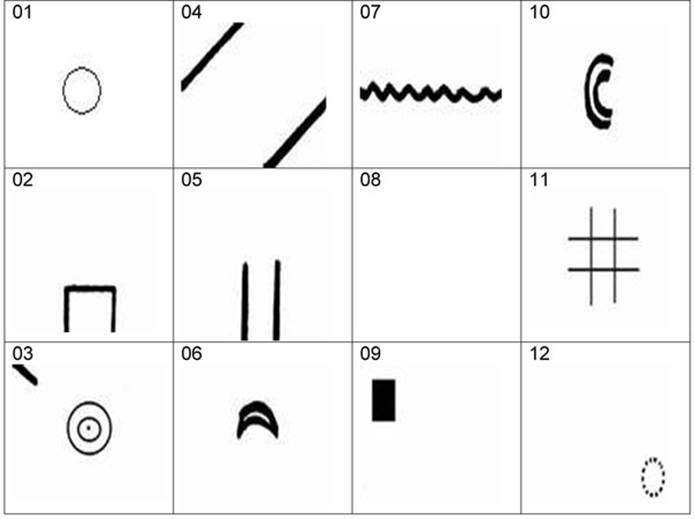 Надеемся, наши пояснения помогут вам правильно оценивать ваших сотрудников, четче понимать их психотип и лучше налаживать с ними отношения.

Распределение хи-квадрат — Терминология шести сигм

Термины шести сигм

Тест хи-квадрат — это статистический инструмент, используемый для проверки независимости или зависимости (или согласия) между случайными величинами, взятыми из разных совокупностей. Критерий хи-квадрат также можно использовать для проверки соответствия между наблюдаемым распределением частот и ожидаемым распределением частот. С помощью теста хи-квадрат вы сравниваете целевую дисперсию с наблюдаемой дисперсией. Он используется для проверки независимости двух номинальных переменных. Помните, что номинальные переменные — это только имена или категории.

---

Тест хи-квадрат — это статистический инструмент, используемый для проверки независимости или зависимости (или согласия) между случайными величинами, взятыми из разных совокупностей. Критерий хи-квадрат можно также использовать для проверки соответствия между наблюдаемых частотных распределений и ожидаемых частотных распределений . С помощью теста хи-квадрат вы сравниваете целевую дисперсию с наблюдаемой дисперсией. Он используется для проверки независимости двух номинальных переменных. Помните, что номинальные переменные — это только имена или категории. Номинальные переменные могут быть шкалой чисел, символов или имен для обозначения различных подклассов. Например, цвета.

При использовании критерия хи-квадрат ассоциации/независимости вы собираетесь вычислить статистику критерия хи-квадрат. И вы собираетесь сравнить эту тестовую статистику с критическим значением хи-квадрат, взятым из таблицы, из Интернета или из программного обеспечения. Как и другие тесты, такие как F-тест и t-тест, вы либо отклоните нулевую гипотезу, либо не сможете отклонить нулевую гипотезу. В любом случае, вы чему-то научитесь. Если вы отвергнете нулевую гипотезу, вы сделаете вывод, что имеется достаточно доказательств, чтобы заключить, что — это зависимость между двумя случайными величинами.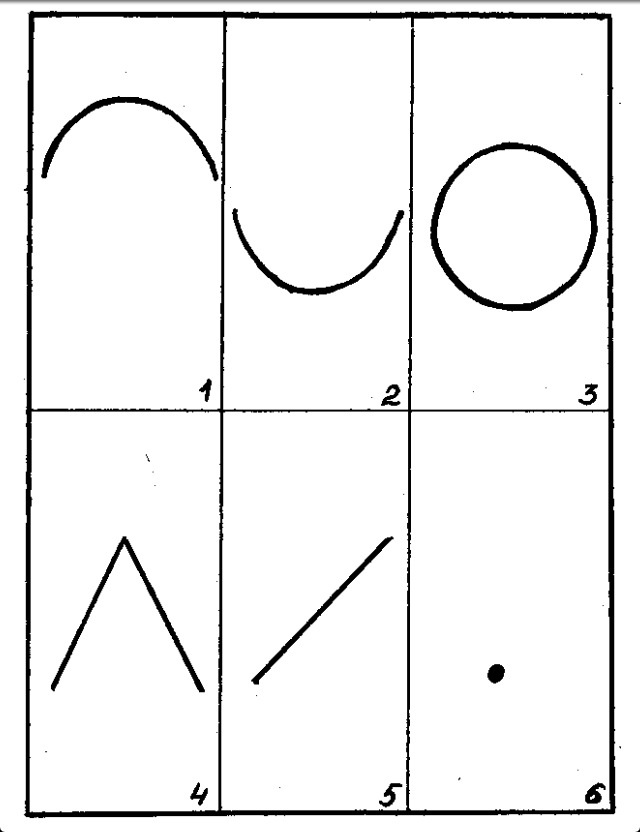 Если, с другой стороны, вы не сможете отклонить нулевое значение, вы сделаете вывод о том, что недостаточно доказательств, чтобы заключить, что две случайные величины значительно отличаются друг от друга. Другими словами, две случайные величины не зависят друг от друга.

Использование: Человеку свойственно хотеть знать, что лучше, что хуже, или просто отличается друг от друга. Возможно, вы можете вспомнить время, когда вы нашли что-то ироничное. Вы думали, что это так, а оказалось по-другому. Может быть, вы подошли к кому-то на улице сзади, думая, что это друг, а когда они обернулись, к вашему большому удивлению, это был кто-то, кого вы даже не знаете. Тест ассоциации/независимости хи-квадрат предназначен для проверки этих аномалий. Вы могли бы подумать, что две случайные величины, взятые из двух разных популяций, будут зависеть друг от друга — и, возможно, окажется, что они зависят друг от друга. В других случаях вы можете подумать, что две случайные величины из разных совокупностей независимы друг от друга, и вы обнаружите, что они не независимы (другими словами, ЗАВИСИМЫ).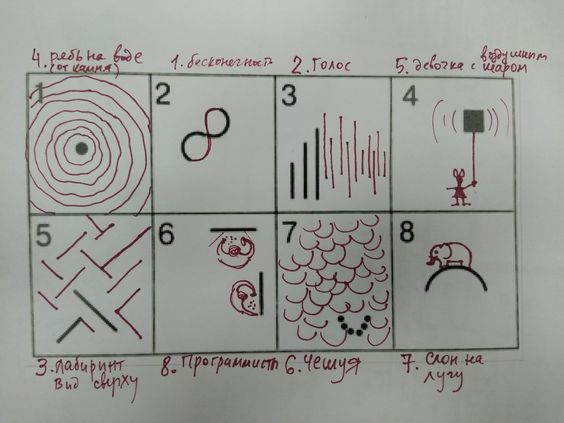 Тест хи-квадрат, использующий распределение хи-квадрат, может разобраться в этом для вас.

Распределение хи-квадрат и проверка гипотез

Распределение хи-квадрат (χ2) является лучшим методом проверки дисперсии генеральной совокупности относительно известного или предполагаемого значения генеральной совокупности. Распределение хи-квадрат — это непрерывное распределение со степенями свободы. Лучшая часть распределения хи-квадрат заключается в том, что оно описывает распределение суммы квадратов случайных величин. Он также используется для проверки качества соответствия распределения данных, независимости ряда данных и для оценки достоверности дисперсии и стандартного отклонения случайной величины от нормального распределения.

История хи-квадрата

Карл Пирсон (1857 – 1936), отец современной статистики (он основал первый в мире отдел статистики в Университетском колледже Лондона), придумал распределение хи-квадрат. Работа Пирсона в статистике началась, когда он разработал математический метод изучения процесса наследственности и эволюции. Позже появилось распределение хи-квадрат, когда Пирсон попытался найти меру согласия других распределений со случайными величинами в своей модели наследственности.

Статистика хи-квадрат

Распределение хи-квадрат может иметь наклон вправо или с длинным хвостом в сторону больших значений распределения. Общая форма распределения будет зависеть от количества степеней свободы в данной задаче. Степень свободы на единицу меньше объема выборки.

Свойства хи-квадрата

• Среднее значение распределения равно количеству степеней свободы: μ=ϑ.
• Дисперсия равна удвоенному числу степеней свободы: σ2 = 2*ϑ.
• Если количество степеней свободы больше или равно 2, максимальное значение Y достигается при χ2=ϑ-2.
• По мере увеличения степеней свободы кривая хи-квадрат приближается к нормальному распределению.
• По мере увеличения степеней свободы увеличивается и симметрия графа.
• Наконец, он может быть смещен вправо, а поскольку случайная величина, на которой он основан, является квадратичной, она не имеет отрицательных значений. По мере увеличения степеней свободы функция плотности вероятности начинает приобретать симметричную форму.

Формула для функции плотности вероятности распределения хи-квадрат:

Где ϑ — параметр формы, а Γ — гамма-функция.

Формула гаммы
Функция равна

Хи-квадрат (χ

² ) Проверка гипотезы

Обычно цель команды шести сигм состоит в том, чтобы найти уровень вариации выходных данных, а не просто среднее значение генеральной совокупности. Прежде всего, команда хотела бы знать, насколько производственный процесс отличается от цели, чтобы увидеть, какие изменения необходимы для достижения процесса без дефектов.

Для сравнения нескольких выборочных дисперсий или сравнения пропорций частот будет использоваться стандартная тестовая статистика, называемая критерием Хи-квадрат χ2. Итак, распределение статистики хи-квадрат называется распределением хи-квадрат.

Типы тестов хи-квадрат для гипотез

Существует два основных типа тестов хи-квадрат:

• Тест независимости хи-квадрат : Определяет наличие связи между двумя категориальными переменными путем сравнения наблюдаемых и ожидаемых частоты результатов теста, когда нет определенной дисперсии генеральной совокупности.
• Критерий дисперсии хи-квадрат: Сравните дисперсии, когда известна дисперсия генеральной совокупности.

Критерий независимости хи-квадрат

Критерий независимости хи-квадрат определяет, существует ли связь между двумя категориальными переменными (такими как пол и выбор курса). Например, тест независимости хи-квадрат исследует связь между одной категорией, такой как пол (мужской и женский), и другой категорией, такой как процент прогулов в школе. Критерий независимости Хи-квадрат является непараметрическим критерием. Другими словами, вам не нужно предполагать нормальное распределение для выполнения теста.

Тест хи-квадрат использует таблицу непредвиденных обстоятельств для анализа данных. Каждая строка показывает категории одной переменной. Точно так же каждый столбец показывает категории другой переменной. Каждая переменная должна иметь две или более категории. Каждая ячейка отражает общее количество случаев для определенной пары категорий.

Предположения критерия независимости хи-квадрат

• Переменные должны быть номинальными или категориальными
• Категории переменных являются взаимоисключающими
• Метод выборки представляет собой простую случайную выборку
• Данные в таблице непредвиденных обстоятельств являются частотами или количеством

Этапы выполнения критерия независимости хи-квадрат

Шаг 1. Определение нулевой гипотезы и альтернативной гипотезы переменные

• Альтернативная гипотеза (H ₁ ): существует значительная связь между двумя категориальными переменными

Шаг 2: укажите уровень значимости

Шаг 3: вычислите статистику χ2

• O — наблюдаемая частота
• E — ожидаемая частота

Ожидаемая частота вычисляется для каждой ячейки = (частота столбцов * частота строк)/ n

Шаг 4: Расчет степени свободы = (количество строк -) * (количество столбцов -1)= (r -1) * (c-1)

Шаг 5: Найдите критическое значение на основе степеней свободы

Шаг 6: Наконец, сделайте статистический вывод: если значение тестовой статистики больше критического значения, отклоните нулевую гипотезу, и, следовательно, мы можем сделать вывод о наличии значительной связи между двумя категориальными переменными.

Критерий независимости Хи-квадрат Пример

Пример: 1000 учащихся средней школы спрашивают, какой их любимый супергерой: Супермен, Железный человек или Человек-паук. При уровне достоверности 95% вы бы пришли к выводу, что существует связь между полом и персонажами супергероев?

• Нулевая гипотеза (H ₀ ): нет никакой связи между полом и любимыми персонажами супергероев.
• Альтернативная гипотеза (H ₁ ): существует значительная связь между полом и любимыми персонажами супергероев.

Уровень значимости: α=0,05:

Сначала рассчитайте ожидаемую частоту:

Для ячейки (Мальчики, Супермен) = (200 * 600)/ 1000 = 120

Аналогичным образом определите ожидаемую частоту всех ячеек :

Степени свободы = (r – 1) * (c – 1) = (2 – 1) * (3 – 1) =2

Критическое значение хи-квадрат для 2 степеней свободы =5,991

Статистика теста значение больше критического значения; следовательно, мы можем отвергнуть нулевую гипотезу.

Итак, мы можем сделать вывод, что существует значительная связь между полом и любимыми персонажами супергероев.

Загрузить тест независимости Хи-квадрат Excel Exemplar

Разблокировать дополнительный контент только для зарегистрированных пользователей!

Чтобы разблокировать дополнительный контент, перейдите на полноценную подписку.

Обновление до полного членства

Если вы зарегистрированы, вы можете войти здесь.

Тест хи-квадрат — сравнение отклонений

Тест хи-квадрат — лучший вариант для двух приложений.

• Случай I: сравнение дисперсий, когда известна дисперсия генеральной совокупности.
• Случай II: Сравнение наблюдаемой и ожидаемой частоты результатов теста при наличии неопределенной популяции.

Когда совокупность подчиняется нормальному распределению, проверка гипотезы используется для сравнения дисперсии совокупности σ _x ² . Тест определяется как:

Где количество выборок равно n, а выборочная дисперсия равна s ² . Форма распределения χ ² похожа на нормальную кривую, но она несимметрична и зависит от степеней свободы.

Проверка гипотезы

Гипотеза с хвостом — это предположение о параметре совокупности. Предположение может быть или не быть верным. Односторонняя гипотеза — это тест, в котором область отклонения находится только в одном направлении. В то же время двусторонняя гипотеза проверяется на альтернативу, согласно которой фактическая дисперсия больше или меньше определенного значения. Выбор одно- или двусторонних тестов зависит от задачи.

Левый хвост и правый хвост χ ² распределение:

Критерий хи-квадрат имеет следующие особенности:

• Оценивает дисперсию выборки
• Неотрицательный.
• Несимметричный.
• Степень свободы при работе с одной дисперсией генеральной совокупности равна n-1.
• Вам не нужны знания об изменчивости населения

Пример теста левостороннего хи-квадрата

Среднее стандартное отклонение времени ожидания авиапассажиров в одной очереди составляет 16 минут. Соответственно, дисперсия населения составляет 256 (квадрат стандартного отклонения). Среднее стандартное отклонение времени ожидания для отдельных очередей с 7 пассажирами составляет 8 минут. Таким образом, выборочная дисперсия равна 64 (квадрат стандартного отклонения). Проверьте, соответствует ли сокращенное время ожидания 95% уровень достоверности.

Нулевая гипотеза H ₀ : σ ₁ ² ≥ (16) ²

Альтернативная гипотеза H _{1 90 110 : σ 1 ² < (16) ²}

Давайте посмотрим на таблицу хи-квадрат. Поскольку S меньше σ, это левый хвостовой критерий, поэтому df =7-1=6. Критическое значение для достоверности 95% составляет 1,63.

Тестовая статистика (1.5) меньше критического значения (1.63) и находится в области отклонения. Следовательно, нулевая гипотеза должна быть отвергнута. Время ожидания уменьшилось с отдельной строкой.

Пример 1:

Компания Barnes производит DVD-плеер и утверждает, что среднее количество часов использования до ремонта составляет 400 часов со стандартным отклонением 10 часов.

Разблокируйте дополнительный контент только для зарегистрированных пользователей!

Чтобы разблокировать дополнительный контент, перейдите на полноценную подписку.

Обновление до полного членства

Если вы зарегистрированы, вы можете войти здесь.

Пример теста хи-квадрата с правосторонним хвостом

Производитель умных часов получил жалобы клиентов на модель XYZ, батарея которой работает меньше времени, чем предыдущая модель. Разница времени автономной работы предыдущей модели составляет 49часы. Было протестировано одиннадцать часов, и стандартное отклонение времени автономной работы составило 9 часов. Предполагая, что данные распределены нормально, может ли заявление об увеличении производительности новой модели быть подтверждено с уровнем достоверности 5%?

Стандартное отклонение популяции σ ₁ ² = 49 часов σ ₁ ^{= 7}

Стандартное отклонение выборки = 9 часов

Нулевая гипотеза H ₀ : σ ₁ ²  ≤ (7 ) ²

Альтернативная гипотеза: H ₁ : σ ₁ ²  > (7) ²

Давайте посмотрим на таблицу Хи-квадрат. Поскольку S больше, чем σ, это правосторонний тест, поэтому df = 11 – 1 = 10. Критическое значение для достоверности 95% составляет 18,307.

Статистика теста:

Статика теста меньше критического значения и не находится в области отклонения. Следовательно, нам не удалось отвергнуть нулевую гипотезу.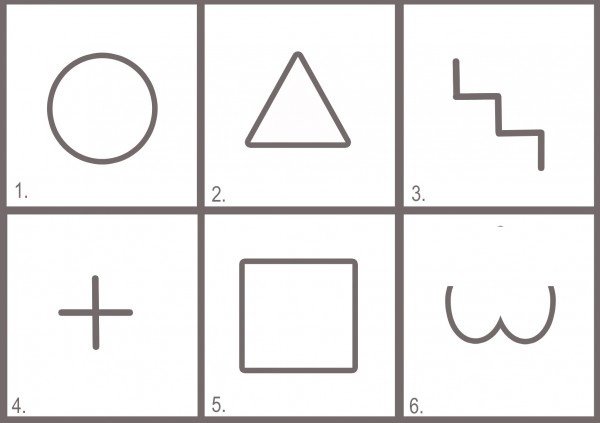 Нет достаточных доказательств, чтобы утверждать, что батарея новой модели работает лучше.

Пример теста двустороннего хи-квадрата

Отдел кадров компании считает, что разница в заработной плате команды, занимающейся новыми цифровыми технологиями, не такая, как у команды, занимающейся технологиями Java. Исторические данные показывают, что стандартное отклонение заработной платы команды Java составляет 49 тысяч долларов. Была собрана заработная плата 30 новых сотрудников, занимающихся цифровыми технологиями, и ее стандартное отклонение составляет 70 тысяч долларов. Предполагая, что данные распределены нормально, можно ли подтвердить утверждение HR с достоверностью 95%?

Стандартное отклонение населения σ ₁ ^{= 49}

Стандартное отклонение выборки = 70

Нулевая гипотеза H 60 2

Альтернативная гипотеза H ₁ : σ ₁ ² ≠ (49) ²

df = 30 – 1 = 29.

Поскольку s не равно σ, это двухсторонний тест. Таким образом, α/2 = 0,05/2 = 0,025

Для 29 степеней свободы левый хвост (1-α/2 = 1-0,025 = 0,975) равен 16,047

А правый хвост α/ 2 = 0,025 равен 45,722

Статика теста больше 45,722 и находится в области отклонения. Следовательно, мы можем отвергнуть нулевую гипотезу.

Размер выборки хи-квадрат

Тесты хи-квадрат чувствительны к изменениям размера выборки. Если размер выборки больше, то абсолютные различия становятся все меньшей и меньшей долей ожидаемого значения. Другими словами, сильной связи может не быть, если размер выборки мал, а результаты незначимы, даже если они статистически значимы.

Где…

• n — размер выборки с поправкой
• n’ — размер выборки без коррекции непрерывности
• P ₁ и P ₂ — пропорции в каждой группе
• Q ₁ =1-P ₁
• P̅ = P ₁ +P ₂ /2

Видео хи-квадрат

https://www.youtube.com/watch?v=53kYOOr5Yhk

Таблицы хи-квадрат

• Национальный институт стандартов и технологий
• Хорошая одностраничная брошюра Chi-Square от муниципального колледжа Ричленда
• https://people.richland.edu/james/lecture/m170/tbl-chi.html
• https://www.statisticshowto.datasciencecentral.com/tables/chi-squared-table-right-tail/
• https://www.socscistatistics.com/tests/chisquare2/default2.aspx

Расчет размера выборки хи-квадрат

• https://stats. stackexchange.com/questions/340291/estimate-sample-size-for-chi-squared-test
• http://www.statskingdom.com/sample_size_chi2.html

Другие варианты использования хи-квадрата

• Хи-квадрат критерия согласия : Это проверка статистической гипотезы для проверки того, насколько хорошо выборочные данные соответствуют характеристикам совокупности.
• Таблица непредвиденных обстоятельств Хи-квадрат.

Сертификация «Черный пояс шести сигм» Хи-квадрат Вопросы:

Вопрос: Считается, что время срабатывания отказобезопасного устройства представляет собой дискретное равномерное распределение от 1 до 5 секунд. Для проверки этой гипотезы было проведено 100 тестов с результатами, показанными ниже.

Основываясь на этих данных, каковы значение хи-квадрата (c2) и число степеней свободы (df)?

(A) (c2) значение = 57,5, степени свободы = 4
(B) (c2) значение = 57,5, степени свободы = 5
(C) (c2) значение = 1150,0, степени свободы = 4
(D) (c2) значение = 1150,0, степени свободы = 5

Ответ:  

Разблокируйте дополнительный контент только для зарегистрированных пользователей!

Чтобы разблокировать дополнительный контент, перейдите на полноценную подписку.