Колыбель Ньютона – отличный сувенир для снятия стресса
Всем привет!
В сегодняшнем обзоре пойдет речь о маятнике (колыбель, шары) Ньютона, кому интересно прошу под кат
Начнём с небольшой предыстории.
Я очень увлекаюсь такой наукой как «психология», а как известно психология тесно связана с психиатрией — отраслью медицины, назначение которой распознавание и лечение психических расстройств, а маятник Ньютона это самый простой и эффективный способ снять стресс даже на рабочем месте, а ещё это очень красивый сувенир который отлично украшает рабочее место, создавая атмосферу гармонии и порядка.
Я давно хотела его приобрести для украшения рабочего стола, но появилась возможность взять его обзор и я не стала её упускать 🙂
История появления шаров Ньютона
Колыбель Ньютона (маятник Ньютона) — механическая система, названная в честь Исаака Ньютона для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо.
В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо.
При отклонении первого шарика данной системы и последующим его возвратом к изначальному положению, его энергия и импульс передадутся без изменения через три средних шарика последнему, который приобретёт ту же скорость и поднимется на ту же высоту. Он в свою очередь передаст свой импульс и энергию по цепочке снова первому шарику. Крайние маятники будут колебаться, а промежуточные будут неподвижны. Из-за потерь механической энергии вследствие работы сил трения и упругости колебания маятников затухают, так как в реальных механических системах всегда действуют диссипативные силы.
Чтобы найти скорости шаров после упругого столкновения, надо записать уравнение закона сохранения импульса для такой системы и уравнение закона сохранения энергии и решить полученную систему уравнений. Результат известен: движущийся шар останавливается, а покоящийся приобретает скорость первого
Теперь можно перейти и к самому товару.
Основа пластмассовая, шарики и стойка металлические, шарики подвешены на леске.
Товар пришел вот в такой коробке
При транспортировке коробка помялась, но несмотря на это товар целый.
После того как открыла коробку началось самое интересное, леска на которых висят шарики очень сильно запуталась и местами она даже была связана и вечер был посвящен ее распутыванию.
Внешний вид
На опорах есть высечки для лески.
Шарики как я уже писала выше металлические.
Вес и диаметр шариков
Низ пластмассовый на резиновых ножках
Как действуют шары Ньютона?
Для того чтобы увидеть, как этот сувенир работает, достаточно взять один из крайних шариков, отвести его в сторону, а затем отпустить. После того как он ударится об своего соседа, с противоположной стороны произойдет зеркальное отображение данного движения, причем в том же ритме и с той же скоростью. Шарики посередине остаются неподвижными, а крайние будут колебаться до тех пор, пока силы упругости и трения не приведут к медленной остановке движения. Ритмичность движения и звуков как раз и создает эффект расслабления и стимулирует медитацию человека. Как долго будут двигаться шары Ньютона? Продолжительность работы такого оригинального подарка напрямую зависит от веса и размера шариков: чем больше их диаметр и чем они тяжелее, тем дольше будет длиться данный процесс, и наоборот.
Шарики посередине остаются неподвижными, а крайние будут колебаться до тех пор, пока силы упругости и трения не приведут к медленной остановке движения. Ритмичность движения и звуков как раз и создает эффект расслабления и стимулирует медитацию человека. Как долго будут двигаться шары Ньютона? Продолжительность работы такого оригинального подарка напрямую зависит от веса и размера шариков: чем больше их диаметр и чем они тяжелее, тем дольше будет длиться данный процесс, и наоборот.
Видео
На этом хотела бы закончить свой обзор и в конце сказать, что товаром довольна — «прикольная игрушка», но к сожалению через пару недель звук бьющихся шариков мне надоел, но как украшение рабочего места нравится.
Цена с купоном ToysHo $12.87.
Спасибо за внимание и хороших вам покупок! 🙂
Товар предоставлен для написания обзора магазином. Обзор опубликован в соответствии с п.18 Правил сайта.
Обзор опубликован в соответствии с п.18 Правил сайта.
Надувной аттракцион Колыбель Ньютона в аренду на праздник
Командные игры
Минимальный возраст
от 14 лет
Габариты
8,1 м х 6,2 м х 4,0 м
Проходимость, чел/ч
до 300
Потребляемая мощность
3 кВт
Вес, кг
215
Доставка
Стоимость доставки не включена в стоимость аренды и зависит от общей суммы заказа.
Описание товара
В Колыбеле Ньютона участнику одной команды нужно пробежать по прямой, а вторая команда пытается сбить его мешками с мягким наполнителем. В случае падения, героя ждёт встреча с надувным батутом, так что всё крайне безопасно. Так что этот аттракцион превращается в настоящее сражение. Станет хорошим дополнением в программу тимбилдинга и развлечёт гостей на спортивном празднике.
Возврат к списку
Колыбель(маятник) Ньютона | Компьютерная графика
Колыбель Ньютона (маятник Ньютона) — механическая система, названная в честь Исаака Ньютона для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо, поскольку колебания маятника совершаются под действием силы тяжести, силы упругости и силы трения.
В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо, поскольку колебания маятника совершаются под действием силы тяжести, силы упругости и силы трения.
Это изобретение, придуманное Саймоном Пребблом в 1967 году, а сегодня часто встречаемую на письменных столах в кабинетах и офисах, можно поместить и в музей физики. Знание того, что она иллюстрирует законы сохранения импульса и сохранения энергии не только не помешает, но и придаст особый смысл наблюдению.
При отклонении первого шарика данной системы и последующим его возвратом к изначальному положению, его энергия и импульс передадутся без изменения через три средних шарика последнему, который приобретёт ту же скорость и поднимется на ту же высоту. Он в свою очередь передаст свой импульс и энергию по цепочке снова первому шарику. Крайние маятники будут колебаться, а промежуточные будут неподвижны. Из-за потерь механической энергии вследствие работы сил трения и упругости колебания маятников затухают, так как в реальных механических системах всегда действуют диссипативные силы.
Чтобы найти скорости шаров после упругого столкновения, надо записать уравнение закона сохранения импульса для такой системы и уравнение закона сохранения энергии и решить полученную систему уравнений. Результат известен: движущийся шар останавливается, а покоящийся приобретает скорость первого.
В колыбели Ньютона первый шарик передаёт импульс второму шарику и останавливается. Второй шарик получает импульс потенциальной энергии от первого, но из-за невозможности преобразования потенциальной энергии в кинетическую, импульс переходит от второго маятника далее — в третий, четвертый, пятый. Последний шарик не имеет перед собой, кому передать свой импульс, поэтому свободно движется, поднимаясь на высоту h, затем возвращается, и всё повторяется в обратном направлении.
Колыбель Ньютона — это… Что такое Колыбель Ньютона?
Колыбель Ньютона
Шарики Ньютона (маятник Ньютона) — механическая система, придуманная Исааком Ньютоном для демонстрации преобразования энергии различных видов друг в друга: кинетической в потенциальную и наоборот. В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо.
В отсутствие противодействующих сил (трения) система могла бы действовать вечно, но в реальности это недостижимо.
История
Эту популярную игрушку-сувенир, придуманную английским актёром Саймоном Пребблом в 1967 году, а сегодня часто встречаемую на письменных столах в кабинетах и офисах, можно поместить и в музей физики. Можно бесконечно долго играть с ней, глядя на качающиеся шарики (как смотреть на текущую воду или огонь). Но знание того, что она иллюстрирует законы сохранения импульса и сохранения энергии не только не помешает, но и придаст особый смысл наблюдению.
Если отклонить первый шарик и отпустить, то его энергия и импульс передадутся без изменения через три средних шарика последнему, который приобретёт ту же скорость и поднимется на ту же высоту. Он в свою очередь передаст свой импульс и энергию по цепочке снова первому шарику. Крайние маятники будут колебаться, а средние шарики будут покоиться. Если бы не было потерь механической энергии вследствие работы сил трения и упругости, то колебания продолжались бы вечно, но они затухают, так как в реальных механических системах всегда действуют диссипативные силы.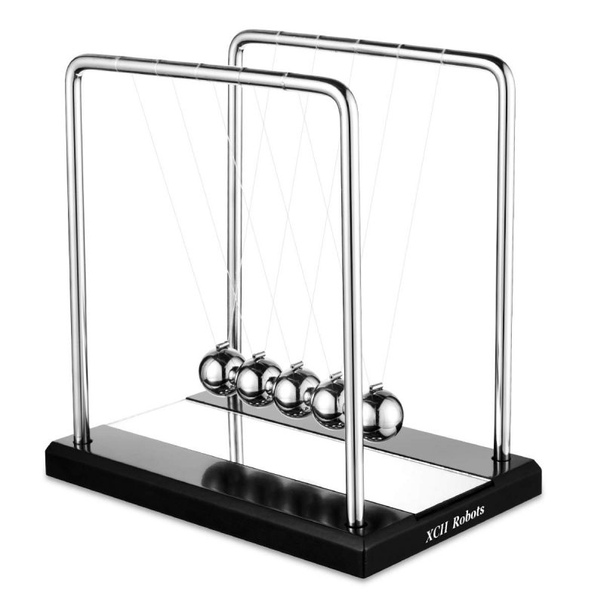
Интересным является то, что первый шарик передаёт импульс последнему не непосредственно, а через средние шарики, которые остаются неподвижными. Картина напоминает распространение упругой волны в твёрдом теле, то есть передачу упругих возмущений и энергии упругой деформации без переноса вещества (например, звук).
Рассмотрим простой случай, когда движущийся шар сталкивается с таким же покоящимся шаром («Колыбели Ньютона» всего из двух шариков). Столкновение упругое и центральное (именно такое наблюдается в идеальной «Колыбели Ньютона»). Чтобы найти скорости шаров после упругого столкновения, надо записать уравнение закона сохранения импульса для такой системы и уравнение закона сохранения энергии и решить полученную систему уравнений. Результат известен: движущийся шар останавливается, а покоящийся приобретает скорость первого.
В колыбели Ньютона первый шарик передаёт импульс второму шарику и останавливается. Мы не видим, как второй шарик получает импульс от первого, не «видим» его скорость. Но, если присмотреться: шарик чуть заметно «вздрагивает», то есть он движется с полученной скоростью, но на маленьком пути «из-за тесноты». Но он успевает на этом коротком пути отдать импульс третьему шарику и остановиться. То же с третьим шариком и т. д. Последний шарик не имеет перед собой, кому передать свой импульс, поэтому свободно движется, поднимаясь на высоту h, затем возвращается, и всё повторяется в обратном направлении.
Но, если присмотреться: шарик чуть заметно «вздрагивает», то есть он движется с полученной скоростью, но на маленьком пути «из-за тесноты». Но он успевает на этом коротком пути отдать импульс третьему шарику и остановиться. То же с третьим шариком и т. д. Последний шарик не имеет перед собой, кому передать свой импульс, поэтому свободно движется, поднимаясь на высоту h, затем возвращается, и всё повторяется в обратном направлении.
Изготовление
«Колыбель Ньютона» можно изготовить самостоятельно. Шарики надо подвешивать на двух под углом друг к другу нитях, чтобы плоскость колебаний шариков сохранялась постоянной, и удары были центральными.
В мире
Самая большая Колыбель Ньютона в мире находится в г. Kalamazoo (штат Мичиган, США). В ней 16 боулинг-шаров, массой 6,8 кг каждый, подвешенных на нитях длиной 6,1 м на высоте 1 м от пола.
Варианты
Квантовый
При помощи интерферирующих лазерных лучей создаются тысячи «трубок»-ловушек. В каждую трубку, созданную лазерным лучом, помещаются приблизительно 150 атомов (в трубке они могут двигаться только в одном измерении). Затем атомы лазером же охлаждаются до миллиардных долей градуса (в Кельвинах). После лазером половине атомов придаётся один импульс, а половине – противоположный. В результате получается вариант, когда даже после 10 000 столкновений каждый атом колеблется с исходной амплитудой[1]
Затем атомы лазером же охлаждаются до миллиардных долей градуса (в Кельвинах). После лазером половине атомов придаётся один импульс, а половине – противоположный. В результате получается вариант, когда даже после 10 000 столкновений каждый атом колеблется с исходной амплитудой[1]
Эволюция маятника Ньютона
http://www.diary.ru/~fizik-romantik/p158123288.htm
Примечания
См. также
Ссылки
- Статья, Колыбель Ньютона в школьном музее физики
Колыбель Ньютона в новой интерпретации
В предыдущей статье я рассказывала о колыбели для малышей, а теперь предлагаю вашему вниманию «Колыбель Ньютона» в новой интерпретации.
Кто со школьной скамьи не знает популярную игрушку, которая демонстрирует преобразование одной энергии в другую: кинетической в потенциальную и наоборот. Когда-то механическую систему, состоящую из подвешенных на нитях шариков, придумал Исаак Ньютон.
А в 1967 году английский актер Саймон Преббл дал Ньютоновской установке новую жизнь. Теперь это распространенный офисный сувенир, который часто служит предметом для релаксации. Считается, что движение и постукивание шариков действует на человека расслабляюще.
Как бы не использовалась Колыбель Ньютона в наше время, суть системы — иллюстрировать законы физики. А вот японскому студенту-дизайнеру Yasutoki Kariya пришла в голову мысль усовершенствовать Ньютоновскую модель, используя современные методы программирования. Вместо металлических шариков для наглядности в инсталляции используются лампочки.
В новой интерпретации Колыбель Ньютона имитирует передачу света и движения от одного конца ряда лампочек к другим. Бегущее пятнышко света не только расслабляет, но и завораживает. Включение и выключение ламп происходит с помощью запрограммированных нужным образом датчиков.
В результате новая Колыбель Ньютона больше похожа на колыбель Эдисона и создает всего лишь иллюзию передачи энергии. Дизайнер Yasutoki Kariya назвал, созданную им арт-инсталляцию, Asobi, что в переводе означает «игра».
Дизайнер Yasutoki Kariya назвал, созданную им арт-инсталляцию, Asobi, что в переводе означает «игра».
Наблюдая за игрой света, как будто попадаешь на гипнотический сеанс. В этом году Колыбель Ньютона в новой интерпретации стала одним из кандидатов на премию «Designer Junior» от компании Mitsubishi.
Интересности от клуба «Живи интересно»
Как работает колыбель Ньютона? | Исполнительный мяч Clicker
Знаете ли вы его как «Колыбель Ньютона» или «Кликер для руководителей», скорее всего, вы видели настольную игрушку для обучения, которая, кажется, не поддается объяснению. Устройство представляет собой ряд из пяти металлических шариков, расположенных так, чтобы они почти не касались друг друга, которые подвешены к раме на тонких проволоках.
Когда шар на одном конце люльки отрывается от других и затем отпускается, он ударяется о следующий шар в люльке, который остается неподвижным. Но мяч на противоположном конце ряда подбрасывается в воздух, затем раскачивается, чтобы ударить другие шары, снова запуская цепную реакцию в обратном направлении.
Но мяч на противоположном конце ряда подбрасывается в воздух, затем раскачивается, чтобы ударить другие шары, снова запуская цепную реакцию в обратном направлении.
Как работает колыбель Ньютона? Устройство можно объяснить некоторыми фундаментальными принципами физики и механики (теоретизированными сэром Исааком Ньютоном, Рене Декартом и другими).
Колыбель Ньютона хорошо демонстрирует принцип сохранения количества движения (масса, умноженная на скорость). Этот принцип гласит, что при столкновении двух объектов общий импульс объектов до столкновения равен полному импульсу объектов после столкновения.
Другими словами, когда первый шар Колыбели Ньютона сталкивается со вторым, первый шар останавливается, но его импульс не теряется, а просто передается второму шару, затем третьему, затем четвертому, пока не достигнет самый последний бал. Вы наблюдаете это сохранение количества движения, когда последний шар взлетает в воздух с почти тем же импульсом, что и первый шар. Таким образом, если два шара поднять в воздух на одном конце устройства и отпустить, тогда два шара на противоположном конце будут качаться в ответ.
Таким образом, если два шара поднять в воздух на одном конце устройства и отпустить, тогда два шара на противоположном конце будут качаться в ответ.
Этот непрерывный щелчок шариков также является доказательством закона сохранения энергии Ньютона, который гласит, что энергия не может быть создана или уничтожена, но может изменять форму. Колыбель Ньютона достаточно хорошо демонстрирует эту последнюю часть закона, поскольку она преобразует потенциальную энергию одного шара в кинетическую энергию, которая передается по линии шаров и в конечном итоге приводит к качанию вверх последнего шара.
Следуйте за Элизабет Палермо в Twitter @techEpalermo или в Google+.Следите за LiveScience @livescience. Мы также в Facebook и Google+.
Как работают колыбели Ньютона | HowStuffWorks
Здесь есть две последние вещи, и первая — это упругое столкновение. Упругое столкновение происходит, когда два объекта сталкиваются друг с другом, и объединенная кинетическая энергия объектов одинакова до и после столкновения. Представьте на мгновение колыбель Ньютона всего с двумя шарами. Если бы у первого шара было 10 джоулей энергии, и он ударил бы второй шар при упругом столкновении, второй шар отскочил бы с 10 джоулями.Шары в колыбели Ньютона сталкиваются друг с другом в серии упругих столкновений, передавая энергию первого шара по линии на пятый шар, не теряя при этом энергии.
Представьте на мгновение колыбель Ньютона всего с двумя шарами. Если бы у первого шара было 10 джоулей энергии, и он ударил бы второй шар при упругом столкновении, второй шар отскочил бы с 10 джоулями.Шары в колыбели Ньютона сталкиваются друг с другом в серии упругих столкновений, передавая энергию первого шара по линии на пятый шар, не теряя при этом энергии.
По крайней мере, так это работало бы в «идеальной» колыбели Ньютона, то есть в среде, где на шары действуют только энергия, импульс и гравитация, все столкновения абсолютно упругие, а конструкция люльки идеален. В такой ситуации шары продолжали бы качаться бесконечно.
Но невозможно иметь идеальную колыбель Ньютона, потому что одна сила всегда будет действовать, чтобы замедлить вещи до остановки: трение. Трение лишает систему энергии, медленно останавливая шары.
Хотя небольшое трение возникает из-за сопротивления воздуха, основным источником трения являются сами шары. Итак, то, что вы видите в колыбели Ньютона, на самом деле не являются упругими столкновениями, а скорее неупругими столкновениями , в которых кинетическая энергия после столкновения меньше, чем кинетическая энергия до этого. Это происходит потому, что шары сами по себе не идеально эластичны — они не могут избежать эффекта трения. Но из-за сохранения энергии общее количество энергии остается неизменным. Когда шары сжимаются и возвращаются к своей первоначальной форме, трение между молекулами внутри шара преобразует кинетическую энергию в тепло. Шарики также вибрируют, рассеивая энергию в воздухе и создавая щелкающий звук, характерный для колыбели Ньютона.
Это происходит потому, что шары сами по себе не идеально эластичны — они не могут избежать эффекта трения. Но из-за сохранения энергии общее количество энергии остается неизменным. Когда шары сжимаются и возвращаются к своей первоначальной форме, трение между молекулами внутри шара преобразует кинетическую энергию в тепло. Шарики также вибрируют, рассеивая энергию в воздухе и создавая щелкающий звук, характерный для колыбели Ньютона.
Недостатки конструкции люльки также замедляют шары.Если шары не идеально выровнены или имеют не совсем одинаковую плотность, это изменит количество энергии, необходимое для перемещения данного шара. Эти отклонения от идеальной колыбели Ньютона замедляют раскачивание шариков на обоих концах и в конечном итоге приводят к тому, что все шарики раскачиваются вместе в унисон.
Для получения более подробной информации о колыбелях Ньютона, физике, металлах и других связанных предметах, взгляните на следующие ссылки.
Первоначально опубликовано: 17 января 2012 г.
Как сделать простую колыбель Ньютона
Колыбель Ньютона — классический научный проект, демонстрирующий динамику развития. Он также может использоваться как забавная научная игрушка «сделай сам» для детей и взрослых! И psst … он идеально подходит для научной выставки!
У меня особая связь с этим проектом, потому что это был мой собственный выход на научную ярмарку много лет назад. В версии, которую я построил, использовались настоящие шарикоподшипники (преимущество того, что дед был изобретателем в механической мастерской), но вы можете узнать , как построить простую колыбель Ньютона дома , используя материалы из ремесленного магазина, прямо здесь, справа сейчас.
Когда я разрабатывал этот проект для своей книги STEAM Play & Learn и пытался придумать самую простую версию, я экспериментировал с множеством материалов для сфер.Я попробовала деревянные бусины и ГИГАНТСКИЕ пластиковые бусины, и вот что я обнаружила, ни один из них не работал… почему? Ответ кроется в науке, стоящей за этим проектом. МАССА имеет решающее значение для импульса. Узнайте больше об этом в разделе «Давайте поговорим о STEAM» здесь.
МАССА имеет решающее значение для импульса. Узнайте больше об этом в разделе «Давайте поговорим о STEAM» здесь.
Этот пост содержит партнерские ссылки.
Колыбель Ньютона — это проект из моей книги STEAM Play & Learn. STEAM Play & Learn предназначен для дошкольников, но многие проекты, особенно этот и другие проекты электроники в книге, подходят для детей всех возрастов.Вы можете проверить мою книгу на Amazon здесь:
Безопасность: Мрамор — опасность удушья. Пожалуйста, наблюдайте за этим занятием вместе с любым ребенком, который кладет что-нибудь в рот.
ПРИМЕЧАНИЕ. Для работы этого проекта необходимо использовать шарики. Деревянные бусины недостаточно плотны, чтобы передавать через них энергию.
Деревянные бусины недостаточно плотны, чтобы передавать через них энергию.
Материалы
- Jumbo Craft Sticks
- (6) Шарики
- Строка
- Ножницы
- Клей
- Лента
- Карандаш
- Пистолет для горячего клея / клей
Инструкции
- Шаг 1 Клей (4) поделки склеивается по углам, образуя квадрат.Повторите то же самое с еще (4) палочками для поделок. Дайте высохнуть. Это будут стороны рамки.
- Шаг 2 Разрежьте струну на (6) равных частей длиной примерно 8 дюймов
- Шаг 3 Горячим клеем приклейте шарик к центру одного из отрезков веревки. Повторите эти действия, чтобы получить (6) отдельных шариков, каждый из которых приклеен к центру веревки.

- Шаг 4 Сделайте (6) отметок вдоль двух палочек через каждые ½ дюйма. Убедитесь, что отметки на палках находятся по центру.
- Шаг 5 Обмотайте один конец струн шариками, прикрепленными вдоль одной из палочек к каждой отметке.Отложите в сторону.
- Шаг 6 С помощью горячего клея соберите раму. Возьмите две стороны и приклейте горячим клеем палку для поделок перпендикулярно каждому углу. Финальным кадром будет куб.
- Шаг 7 Приклейте палку для поделок с закрепленной лентой веревкой / шариками к одной стороне рамки.
- Шаг 8 Приклейте вторую помеченную палку для поделок к противоположной стороне рамки.
- Шаг 9 Обмотайте свободный конец каждой струны шариком, прикрепленным к отмеченной палочке.Осторожно потяните за струны, чтобы убедиться, что кабели выровнены.
 Шарики должны выровняться как по горизонтали, так и при взгляде сверху.
Шарики должны выровняться как по горизонтали, так и при взгляде сверху.
Потяните один из крайних шариков вверх и отпустите! Смотрите, что происходит!
Давайте поговорим о STEAM
The Science
Колыбель Ньютона — игрушка, названная в честь очень известного ученого сэра Исаака Ньютона. Он демонстрирует научную идею под названием импульс. Импульс — это сила движущегося объекта. Когда вы качаете один из шариков на конце, он сталкивается с шариком рядом с ним, и сила этого столкновения распространяется через каждый из других шариков, пока не достигнет последнего, который качается вверх. Когда этот шарик опускается обратно, сила снова проходит через шарики. Узнайте больше об импульсе и столкновениях здесь.
Это демонстрация научного принципа сохранения импульса . Этот принцип гласит, что когда два объекта сталкиваются, их импульс до столкновения равен их импульсу после столкновения. В Колыбели Ньютона сила столкновения проходит через каждый из шариков, пока не достигнет последнего шарика, который взлетает вверх.
В Колыбели Ньютона сила столкновения проходит через каждый из шариков, пока не достигнет последнего шарика, который взлетает вверх.
Импульс также напрямую связан с массой объекта: Импульс = масса * скорость
При разработке этого проекта я экспериментировал с различными продуктами для сфер. Я надеялся, что пластиковые бусины подойдут, потому что ими было бы намного проще пользоваться. Проблема в том, что у них очень маленькая масса, и поэтому их импульс был не очень сильным, когда они качнулись.Вам нужно использовать материал для сфер, который является плотным и может передавать энергию через него.
Плотность — это мера количества массы на единицу объема объекта. Более плотные объекты имеют большую массу. Чем больше масса у объекта, тем сильнее будет сила импульса при его качании. Вы можете проверить это сами в рамках проекта научной ярмарки! См. Раздел Как превратить это в проект Science Fair ниже.
Инженерное дело
Эта игрушка, сделанная своими руками, поддерживается жестким каркасом. Рама — это конструкция, которая плотно удерживает что-то на месте. Эта игрушка очень подвижна в шариках и не будет работать, если рамка вокруг шариков также будет двигаться.
Рама — это конструкция, которая плотно удерживает что-то на месте. Эта игрушка очень подвижна в шариках и не будет работать, если рамка вокруг шариков также будет двигаться.
Колыбель Ньютона также демонстрирует концепцию под названием допуски . В машиностроении продукты должны быть построены очень точно. В противном случае продукт развалится при использовании. В «Колыбели Ньютона» шарики нужно вешать очень осторожно рядом и выстраивать в линию, иначе игрушка не подойдет.
Другие идеи
Получайте удовольствие, играя с этим! Попробуйте поднять и выпустить по два шарика за раз.Что происходит?
Сначала раскрасьте палочки и узнайте о капиллярном действии! Если вы замочите палочки для поделок в воде, окрашенной пищевым красителем, цвет будет подниматься по дереву по мере впитывания воды. Вы можете узнать, как это сделать, здесь. Дайте высохнуть, а затем сделайте выкрашенную в галстук колыбель Ньютона.
Как превратить колыбель Ньютона в проект Science Fair
Давайте превратим эту тему в настоящий эксперимент! Вот как вы можете представить это на научной выставке:
- Задайте себе вопросы В этом проекте происходит много интересных вещей, которые вы можете исследовать.
 Некоторые идеи для вопросов: какие материалы сферы лучше всего демонстрируют импульс (мрамор, шарикоподшипники, деревянные бусины, жевательные резинки)? Можете ли вы придать деревянным бусинам больше массы, чтобы они работали в этой демонстрации? Как? Насколько жесткой должна быть рама, чтобы проект работал? Влияет ли количество сфер на то, как это работает? Что произойдет, если у вас на линии будет больше сфер? Что будет, если у вас будет меньше?
Некоторые идеи для вопросов: какие материалы сферы лучше всего демонстрируют импульс (мрамор, шарикоподшипники, деревянные бусины, жевательные резинки)? Можете ли вы придать деревянным бусинам больше массы, чтобы они работали в этой демонстрации? Как? Насколько жесткой должна быть рама, чтобы проект работал? Влияет ли количество сфер на то, как это работает? Что произойдет, если у вас на линии будет больше сфер? Что будет, если у вас будет меньше? - Исследование Изучите информацию в Интернете и в библиотеке, чтобы попытаться предсказать ответ на свой вопрос.Например, прочтите об импульсе, массе и плотности. Постарайтесь предсказать, из каких материалов будет получена идеальная модель Колыбели Ньютона.
- Сделайте гипотезу Гипотеза — это ваше предсказание ответа на ваш вопрос, основанное на вашем исследовании. Это может быть правдой, а может и нет.
- Эксперимент! Проверьте свою гипотезу, проверив переменные и задокументировав их.
 Обязательно записывайте каждый эксперимент и то, что происходит; это называется вашими данными.
Обязательно записывайте каждый эксперимент и то, что происходит; это называется вашими данными.
Примеры:
Экспериментируйте с материалами сферы Попробуйте использовать большие деревянные бусины и, если возможно, шариковые подшипники.Как разные материалы меняют работу модели?
Эксперимент с массой Попробуйте использовать один материал для сфер и добавить массу, чтобы посмотреть, влияет ли это на действие. Можете ли вы добавить что-нибудь плотное к нижней части сфер и изменить импульс?
Эксперимент с количеством сфер Будет ли модель работать, если сфер 10? Как насчет 2? Какое идеальное количество сфер использовать для получения наиболее последовательной реакции?
Поэкспериментируйте с тем, как высоко вы поднимете шарики Что произойдет, если вы с трудом поднимете шарики и уроните их? Как это меняет импульс?
- Сделайте вывод На основании ваших экспериментов сделайте вывод.
 Ваша гипотеза верна?
Ваша гипотеза верна? - Поделитесь своими выводами Создайте презентацию со своими выводами. Включите свое исследование, гипотезу, собранные данные и свои выводы. Не забудьте включить изображения и образцы!
Колыбель Ньютона будет интересным проектом для научной выставки! Чтобы узнать больше об идеях Science Fair, загляните в этот список
Хотите больше STEAM?
Если вы хотите увидеть больше проектов из моей книги, переходите сюда.
Вы также можете следить за новостями в Instagram, используя #steamplayandlearn. Если вы попробуете какие-либо сообщения из книги, обязательно пометьте их тегами #steamplayandlearn!
Вы увлечены воспитанием творческих детей?
Присоединяйтесь к более чем 22 179 родителям и педагогам, которые хотят общаться с детьми и развивать их творческий процесс с помощью волшебных, простых проектов, которые вы можете выполнять ВМЕСТЕ.
Подпишитесь на нашу рассылку, чтобы получать идеи проектов, а также предложения по некоторым нашим творческим продуктам.
Если вы хотите прочитать нашу политику конфиденциальности перед подпиской, перейдите сюда.
Введение — Колыбель Ньютона
Введение
http://teachertech.rice.edu/Participants/louviere/Newton/newton5.jpg
Сэр Исаак Ньютон, пожалуй, один из самых
признанные и известные ученые, которые когда-либо жили в истории человечества. Его
открытия и эксперименты в области физики, математики и многих других
науки открыли дверь современной науке.Многие из его идей — результат
наблюдения и прочие — чистого гения. Открытые им законы несут его
имя, и почти наверняка его имя будут помнить поколения
приходить. Это уже подтверждается, поскольку имя «Ньютон» —
символ принципов науки и используется для обозначения идей и изобретений, которые
использовать важные законы природы. Одно такое изобретение, известное как «Ньютон
Колыбель »или« Шары Ньютона »олицетворяет многие из основ Ньютона.
сломать представления о законах, управляющих Вселенной.Несмотря на простоту, он суммирует идеи, которые великий ученый открыл и сделал известными человечеству. . .
http://en.wikipedia.org/wiki/File:Newtons_cradle_animation_book_2.gif
Колыбель Ньютона выглядит очень просто.
устройство; а когда дело доходит до конструкции, его конструкция и сборка довольно тривиальны. Но если присмотреться, можно увидеть, что это устройство изображает
законы физики, которые действительно не так уж бессмысленны. Это устройство явно работает в соответствии с тремя законами Ньютона и распространяется на законы энергии и
импульс.Глубокий анализ этого устройства может легко охватить десятки математических и физических принципов; для того, чтобы содержать информацию, потребуется много книг. Однако этот анализ будет состоять
в первую очередь из принципов сохранения импульса
энергия и их отношение к Колыбели Ньютона. В
Важность импульса и энергии в отношении этого устройства проста: без них шары Ньютона не работали бы и, вероятно, никогда не были бы изобретены. Более того, без законов количества движения и энергии наша Вселенная
Более того, без законов количества движения и энергии наша Вселенная
будет крайне и непредсказуемо отличаться.
Колыбель Ньютона | Кафедра физики
Эта демонстрация используется для демонстрации того, как работает сохранение импульса и энергии с помощью ряда вращающихся сфер. Обычно это система из пяти шаров, прикрепленных к конструкции двумя струнами с каждой стороны. Шар с одного конца поднимается, а когда его отпускают, ударяет по четырем другим шарам. Это столкновение создает силу через другие четыре шара и заставляет шар на другом конце толкать вверх. [1] [2]
Многие спрашивают, почему колыбель не посылает два шара на половину скорости, когда один мяч падает.{2} $$
При неупругом столкновении сохраняется только импульс. Кинетическая энергия, вложенная в систему, действительно работает с чем-то или преобразуется в другую форму энергии, которая часто может выходить из системы. Это не нарушает закон сохранения энергии, поскольку на самом деле энергия не отсутствует, она просто была перемещена в другое место. Обычно эта энергия используется для постоянной деформации объекта, например, для того, чтобы автомобиль смялся при аварии.
Обычно эта энергия используется для постоянной деформации объекта, например, для того, чтобы автомобиль смялся при аварии.
«Колыбель Ньютона» визуализирует упругое столкновение, позволяя ученикам видеть массу как количество шаров, а скорость как высоту, по которой они перемещаются.{2} $$
Решая для скорости $ \ LARGE {v} $, находим:
$$ v_ {out} = \ sqrt {2gh} $$
Почему столько же мячей?
Давайте рассмотрим случай, когда два шара падают и сталкиваются с оставшимися шарами. Как обсуждалось выше, когда шары сталкиваются, импульс должен сохраняться. Итак, мы знаем, что:
$$ m_ {2 мяча} v_ {i} = m_ {? шары} v_ {f} $$
Пытаясь решить что-либо, мы получаем что-то вроде:
$$ v_ {f} = {m_ {2 мяча} \ over m_ {? шары}} v_ {i} $$
Это оставляет нам два неизвестных, конечную массу и конечную скорость, поэтому нам нужно другое уравнение.2} \ over {m_ {? шары}}} $$
Делим обе стороны на $ \ LARGE {m_ {2 шара}} $:
$$ 1 = {{m_ {2 ball}} \ over {m_ {? шары}}} \ поэтому m_ {2 шара} = m_ {? шары} $$
Возвращая это в уравнение количества движения, мы видим, что если масса должна быть одинаковой, то и скорость должна быть такой же:
$$ m_ {2 мяча} v_ {i} = m_ {2 мяча} v_ {f} \ rightarrow v_ {i} = v_ {f} $$
Так всегда бывает с подставкой. Каждый раз, когда с одной стороны падает определенное количество шаров, такое же количество шаров поднимается с другой стороны примерно на одинаковую высоту (что, как было показано, напрямую связано со скоростью).
Каждый раз, когда с одной стороны падает определенное количество шаров, такое же количество шаров поднимается с другой стороны примерно на одинаковую высоту (что, как было показано, напрямую связано со скоростью).
В начало
Колыбель Ньютона Сохранение импульса и энергии
Q4E Пример 7 — Колыбель Ньютона Сохранение импульса и энергии
Предлагаемая тема использования: | ||
Физический уровень A / S, степень по спортивным наукам (1-й, 2-й и 3-й курс) |
Объектив
- Чтобы продемонстрировать сохранение импульса и энергии с помощью колыбели Ньютона
Используемые программные функции Quintic:
|
Введение — Колыбель Ньютона
Колыбель Ньютона состоит из 5 металлических шариков, подвешенных на бифиламентах, чтобы удерживать движение в одной плоскости. Каждый шар настроен так, что в состоянии покоя каждый шар находится в контакте с соседним шаром. Когда конечный шар вынимается из состояния покоя, отводится и отпускается, он качается как маятник и ударяется о следующий шар. При контакте с этим шаром энергия и импульс от первого шара передаются через три покоящихся шара к последнему шару на другом конце.Переданные энергия и импульс заставляют этот шар двигаться с той же скоростью, что и первый шар. Если два или более шарика вытянуты и отпущены, то такое же количество шариков будет вытолкнуто из конца оставшихся шариков.
Импульс определяется как масса, умноженная на скорость.
Импульс = Масса X Скорость
P = Масса X Скорость
Сохранение импульса
Сохранение импульса означает, что импульс системы остается постоянным при условии отсутствия сил трения. Потеря энергии происходит из-за трения, тепла и звука. Например: столкновение, происходящее между снукерным шаром 1 и снукерным шаром 2 в изолированной системе, общий импульс двух объектов до столкновения равен общему импульсу двух объектов после столкновения. Импульс, потерянный шаром 1, равен импульсу, полученному шаром 2.
Потеря энергии происходит из-за трения, тепла и звука. Например: столкновение, происходящее между снукерным шаром 1 и снукерным шаром 2 в изолированной системе, общий импульс двух объектов до столкновения равен общему импульсу двух объектов после столкновения. Импульс, потерянный шаром 1, равен импульсу, полученному шаром 2.
Метод
Колыбель Ньютона была снята на частоте 100 Гц в течение 30 секунд, при различных начальных условиях.Затем каждое видео было откалибровано, и каждый мяч автоматически оцифрован. Затем были применены фильтры Баттерворта для сглаживания данных. Также была измерена масса мяча, чтобы можно было вычислить P (моментум).
Масса мяча = 22 г
Масса мяча = 0,022 кг
Рис. 1. Экспериментальная установка колыбели Ньютона во время испытания с 1 мячом.
Рисунок 2: Угловое смещение рассчитывается путем измерения угла к вертикали
от центра масс шара (COM) до оси 1 COMРисунок 3: Пятый угловой анализ: угловая скорость шара 1 во время испытания 1
Рисунок 4: Пятый угловой анализ: угловая скорость мяча 5 во время испытания 1.
Рис. 5 и 6: Пятый угловой анализ: угловое смещение шара 1 и шара 5 во время испытания 1.
Пробная 1
Первое испытание состояло в запуске маятника путем оттягивания первого шара от покоящегося пакета и его освобождения. Затем люльку снимали до тех пор, пока движение не прекратилось.
Таблицы 1 и 2 показывают угол наклона обоих мячей 1 и 5 к вертикали, скорость обоих мячей и их количество движения во время первых двух качков.Выделенные темным цветом фигуры представляют точку, в которой движущийся мяч ударяется о статические шары. Во время первого замаха максимальный импульс для шара №1 во время его спуска составил 7,472, после контакта с покоящимися шарами импульс и энергия передаются через систему, заставляя шар 5 двигаться и достигать максимального значения импульса 7,515. В таблице 2 и на рисунке 8 показано падение мяча 5 обратно в «неподвижные шары» (качели 2). Таблица 2 показывает, что мяч 5 достигает максимального количества движения 7. 47 в кадре 51 перед ударом по неподвижным шарам, и шар 1 достигает максимального импульса 7,16 в кадре 55. На рисунках 7 и 8 показаны соответствующие кадры .
47 в кадре 51 перед ударом по неподвижным шарам, и шар 1 достигает максимального импульса 7,16 в кадре 55. На рисунках 7 и 8 показаны соответствующие кадры .
| Таблица 1 | Мяч 1 | Мяч 5 | ||||||
Рама | Угол (º) | Скорость (град / сек) | Масса (кг) | Импульс (кг.м / с) | Угол (º) | Скорость (град / сек) | Масса (кг) | Импульс (кг. |
14 | 15,41 | 310,70 | 0,022 | 6,835 | ,26 | ,00 | 0,022 | 0.000 |
15 | 12,22 | 316,68 | 0,022 | 6,967 | ,26 | ,00 | 0,022 | 0,000 |
16 | 9,08 | 339,64 | 0,022 | 7. | ,26 | ,00 | 0,022 | 0,000 |
17 | 5,43 | 337,40 | 0,022 | 7,423 | ,26 | 12,90 | 0,022 | 0,284 |
18 | 2. | 258,44 | 0,022 | 5,686 | ,52 | 91,11 | 0,022 | 2,004 |
19 | ,26 | 142,64 | 0,022 | 3,138 | 2,08 | 220. | 0,022 | 4,859 |
20 | ,52 | 38,89 | 0,022 | 0,856 | 4,94 | 313,41 | 0,022 | 6,895 |
21 | ,52 | 12. | 0,022 | 0,283 | 8,35 | 341,61 | 0,022 | 7,515 |
22 | ,78 | 25,92 | 0,022 | 0,570 | 11,77 | 334,92 | 0. | 7,368 |
23 | 1,04 | 25,92 | 0,022 | 0,570 | 15,05 | 316,77 | 0,022 | 6,969 |
24 | 1,30 | 13,25 | 0. | 0,292 | 18,10 | 289,11 | 0,022 | 6,360 |
Рисунок 7: последовательность из 12 изображений
| Таблица 2 | Мяч 1 | Мяч 5 | |||||||
Рама | Угол (º) | Скорость (град / сек) | Масса (кг) | Импульс (кг. | Угол (º) | Скорость (град / сек) | Масса (кг) | Импульс (кг.м / с) | |
48 | ,52 | ,00 | 0,022 | 0,000 | 16,70 | -292,76 | 0,022 | -6. | |
49 | ,52 | ,00 | 0,022 | 0,000 | 13,66 | -300,00 | 0,022 | -6,600 | |
50 | ,52 | ,00 | 0,022 | 0. | 10,70 | -318,58 | 0,022 | -7,009 | |
51 | ,52 | ,00 | 0,022 | 0,000 | 7,29 | -339,94 | 0,022 | -7,479 | |
52 | . | -51,85 | 0,022 | -1,141 | 3,90 | –299,20 | 0,022 | -6,582 | |
53 | ,52 | -155,47 | 0,022 | -3,420 | 1,30 | -195. | 0,022 | -4,291 | |
54 | 2,59 | -259.60 | 0,022 | -5,711 | ,00 | -78,12 | 0,022 | -1,719 | |
55 | 5,71 | -324. | 0,022 | -7,138 | ,26 | -26,04 | 0,022 | -0,573 | |
56 | 9,08 | -325,52 | 0,022 | -7,161 | ,52 | -13,02 | 0. | -0,286 | |
57 | 12,22 | -316,68 | 0,022 | -6,967 | ,52 | -13,02 | 0,022 | -0,286 | |
58 | 15,41 | -294,38 | 0. | -6,476 | ,78 | -13,02 | 0,022 | -0,286 | |
59 | 18,11 | -269,18 | 0,022 | -5,922 | ,78 | -13,02 | 0,022 | -0. | |
Рисунок 8: последовательность из 12 изображений
Опытная 2
Проба вторая заключалась в запуске маятника двумя шарами. Затем люльку снимали до тех пор, пока движение не прекратилось. Таблицы 3 и 4 показывают угол между шарами 1, 2, 4 и 5 относительно вертикали, скорость, с которой шары движутся, и их максимальный импульс во время первых 2 качелей. Выделенные фигуры (темные) представляют собой точку, в которой движущиеся шары сталкиваются со статическими шарами.Во время первого замаха максимальный импульс для шара 1 и 2 во время его спуска составлял 6,022 и 6,546 соответственно, после контакта с покоящимися шарами импульс и энергия передаются через систему, заставляя шары 4 и 5 двигаться и достигать максимальных значений импульса 6,264 и 6,364 соответственно. В Таблице 4 представлены шары 4 и 5, возвращающиеся в «покоящиеся шары» (качели 2). Таблица 4 показывает, что шары 4 и 5 достигают максимальных импульсов 6,350 и 6,215 на кадрах 53 и 54 соответственно, прежде чем попасть в покоящиеся шары. Шары 1 и 2 достигают максимальных значений импульса 5,756 и 6,015 на кадрах 58 и 57.
Шары 1 и 2 достигают максимальных значений импульса 5,756 и 6,015 на кадрах 58 и 57.
Таблица 3 | Мяч 1 | Мяч 2 | Масса | Мяч 1 | Мяч 2 | Мяч 4 | Мяч 5 | Масса | Мяч 4 | Мяч 5 |
Рамка | Скорость | Скорость | (кг) | Импульс | Импульс | Скорость | Скорость | (кг) | Импульс | Импульс |
16 | 253. | 275,99 | 0,02 | 5,570 | 6.072 | 38,36 | 38,95 | 0,02 | 0,844 | 0,857 |
17 | 252,55 | 286,88 | 0,02 | 5. | 6,311 | 38,37 | 38,89 | 0,02 | 0,844 | 0,855 |
18 | 263.09 | 297,55 | 0,02 | 5,788 | 6,546 | 25,64 | 25. | 0,02 | 0,564 | 0,570 |
19 | 273,72 | 297,54 | 0,02 | 6.022 | 6,546 | 38,71 | 26,21 | 0,02 | 0,852 | 0. |
20 | 208,05 | 246,11 | 0,02 | 4,577 | 5,414 | 103,23 | 78,28 | 0,02 | 2,271 | 1,722 |
21 | 116,88 | 142. | 0,02 | 2,571 | 3,131 | 194,11 | 195,80 | 0,02 | 4,270 | 4,308 |
22 | 65,45 | 51,64 | 0,02 | 1,440 | 1.136 | 259,39 | 274,54 | 0,02 | 5,707 | 6.040 |
23 | 39,46 | 25,79 | 0,02 | 0,868 | 0,567 | 284,73 | 289,28 | .02 | 6,264 | 6,364 |
24 | 39,20 | 38,65 | 0,02 | 0,862 | 0,850 | 273,30 | 265,56 | 0,02 | 6,013 | 5,842 |
25 | 52.24 | 38,62 | 0,02 | 1,149 | 0,850 | 246,33 | 243,51 | 0,02 | 5,419 | 5,357 |
26 | 39,87 | 25,71 | 0,02 | 0.877 | 0,566 | 236,51 | 247,39 | 0,02 | 5.203 | 5,442 |
27 | 39,95 | 26,98 | 0,02 | 0,879 | 0,593 | 230,89 | 235.65 | 0,02 | 5,080 | 5,184 |
Таблица 4 | Мяч 1 | Мяч 2 | Масса | Мяч 1 | Мяч 2 | Мяч 4 | Мяч 5 | Масса | Мяч 4 | Мяч 5 |
Рамка | Скорость | Скорость | (кг) | Импульс | Импульс | Скорость | Скорость | (кг) | Импульс | Импульс |
50 | -26.04 | -51,72 | 0,02 | -0,573 | -1,138 | -251,50 | -255,82 | 0,02 | -5,533 | -5,628 |
51 | -26,04 | -64,72 | 0,02 | -0.573 | -1,424 | -258,91 | -279,09 | 0,02 | -5,696 | -6,140 |
52 | -26,04 | -51,80 | 0,02 | -0,573 | -1,140 | -269,10 | -288.65 | 0,02 | -5,920 | -6,350 |
53 | -38,89 | -39,05 | 0,02 | -0,855 | -0,859 | -282,50 | -287,92 | 0,02 | -6,215 | -6.334 |
54 | -77,69 | -77,71 | 0,02 | -1,709 | -1,710 | -257,50 | -260,06 | 0,02 | -5,665 | -5,721 |
55 | -156,14 | -155.31 | 0,02 | -3,435 | -3,417 | -167,41 | -156,22 | 0,02 | -3,683 | -3,437 |
56 | -233,44 | -246,82 | 0,02 | -5,136 | -5.430 | -64,70 | -38,63 | 0,02 | -1,423 | -0,850 |
57 | -258,98 | -273,41 | 0,02 | -5,698 | -6,015 | -38,64 | -13,01 | .02 | -0,850 | -0,286 |
58 | -261,62 | -247,42 | 0,02 | -5,756 | -5,443 | -37,93 | -26,42 | 0,02 | -0,835 | -0,581 |
59 | -254.10 | -236,43 | 0,02 | -5,590 | -5.201 | -37,78 | -26,00 | 0,02 | -0,831 | -0,572 |
60 | -241,74 | -226,08 | 0,02 | -5.318 | -4,974 | -38,40 | -25,99 | 0,02 | -0,845 | -0,572 |
61 | -225,90 | -213,48 | 0,02 | -4,970 | -4,697 | -12,79 | -38.96 | 0,02 | -0,281 | -0,857 |
Опытная 3
Третье испытание состояло в том, чтобы запустить маятник, оторвав первый, второй и третий шар от покоящегося пакета и выпустив его. Пожалуйста, загрузите документ в формате pdf для получения дополнительной информации (внизу страницы):
Пробная 4
Испытание четыре состояло в запуске маятника, оторвав четыре шара от статики и выпустив их.Пожалуйста, загрузите документ в формате pdf для получения дополнительной информации (внизу страницы):
Сводка
В итоге, чтобы проиллюстрировать, действительно ли люлька Ньютона демонстрирует сохранение линейного количества движения, был вычислен общий импульс активных шаров до и после контакта со статическими шарами. Общий импульс рассчитывался путем сложения индивидуальных скоростей каждого шара, чтобы получить общую активную скорость, затем эта сумма умножалась на массу для вычисления общего количества движения.Общий импульс также использовался для того, чтобы импульсы отдельных шаров в системе могли широко варьироваться, поэтому при вычислении общего количества движения и скорости вероятность ошибки снижается.
Таблица 5 иллюстрирует значения общего количества движения через качание 1, испытание 1 (выделенная желтым цветом строка в каждой таблице представляет точку контакта со статическими шарами). Пик импульса для шара 1 возникает за 4 кадра до контакта со статическими шарами со значением 5,98, после контакта со статическими шарами импульс передается через систему шару 5.Мяч 5 достигает своего пикового импульса 5,56 через 3 кадра после того, как мяч 1 коснулся статической упаковки. Это испытание продемонстрировало эффективность передачи импульса через систему
на 92%.
Таблица 5 | Скорость | Всего | Скорость | Всего |
Рамка | Шарик 1 (град / сек) | Импульс | Шарик 5 (град / сек) | Импульс |
14 | 299.14 | 5,98 | 7.60 | 0,15 |
15 | 298,18 | 5,96 | 21,56 | 0,43 |
16 | 277,65 | 5,55 | 52,93 | 1,06 |
17 | 237.87 | 4,76 | 101,19 | 2,02 |
18 | 187,76 | 3,76 | 157,15 | 3,14 |
19 | 140,07 | 2,80 | 208,56 | 4,17 |
20 | 101.78 | 2,04 | 246,75 | 4,93 |
21 | 73,89 | 1,48 | 269,36 | 5,39 |
22 | 54,27 | 1,09 | 278,54 | 5,57 |
23 | 40.81 | 0,82 | 277,87 | 5,56 |
24 | 31,56 | 0,63 | 270,57 | 5,41 |
Таблица 6 иллюстрирует общие значения количества движения через качание 1, испытание 2. Пиковый импульс для активных шаров возникает за 5 кадров до контакта со статическими шарами со значением 20.60, после контакта со статическими шарами, импульс передается через систему на шар 4 и 5. Шары 4 и 5 достигают своего пикового импульса 18,54 через 3 кадра после того, как шары 1 и 2 первоначально контактировали со статической упаковкой. Это испытание продемонстрировало передачу импульса через систему с эффективностью 90%.
Таблица 6 | Скорость | Скорость | Сумма (1 и 2) | Сумма (1 и 2) | Скорость | Скорость | Сумма (4 и 5) | Сумма (4 и 5) |
Рамка | Мяч 1 | Мяч 2 | Скорость | Импульс | Мяч 4 | Мяч 5 | Общая скорость | Импульс |
16 | 243.71 | 271,24 | 514,95 | 20.60 | 34,27 | 37,93 | 72.20 | 2,89 |
17 | 241,42 | 270.01 | 511,43 | 20,46 | 45,56 | 45.02 | 90,58 | 3,62 |
18 | 225,54 | 253,25 | 478,79 | 19,15 | 69,39 | 66,17 | 135,56 | 5,42 |
19 | 196,56 | 220.11 | 416,67 | 16,67 | 105,44 | 102,45 | 207,89 | 8,32 |
20 | 161.01 | 177.80 | 338,81 | 13,55 | 146,63 | 145,19 | 291.82 | 11,67 |
21 | 127,34 | 136,85 | 264,19 | 10,57 | 183,64 | 183,36 | 366,99 | 14,68 |
22 | 100,40 | 103,89 | 204.30 | 8,17 | 210,15 | 210,13 | 420,28 | 16,81 |
23 | 81,03 | 79,69 | 160,72 | 6,43 | 225,19 | 225.60 | 450,79 | 18.03 |
24 | 67,19 | 61,66 | 128,85 | 5,15 | 231,15 | 232,31 | 463,45 | 18,54 |
25 | 57,59 | 47,54 | 105,13 | 4.21 | 230,84 | 231.60 | 462,43 | 18,50 |
26 | 50,74 | 35,56 | 86,31 | 3,45 | 225,95 | 224,42 | 450,37 | 18.01 |
27 | 45.83 | 24,91 | 70,74 | 2,83 | 217,51 | 212,22 | 429,73 | 17,19 |
Сохранение энергии
Колыбель Ньютона также демонстрирует сохранение энергии; Кинетическую и потенциальную энергию шаров можно рассчитать, используя следующее уравнение:
KE = m * v2 / 2
KE = кинетическая энергия
m = масса
V = скорость
PE = mgh
PE = потенциальная энергия
m = Масса
g = Гравитационная постоянная
h = Высота смещения по вертикали
Вертикальное смещение шара рассчитывается путем измерения максимальной высоты шара COM до линии, которая проходит через шары статического COM.Точки максимальной высоты и скорости были рассчитаны путем экспорта данных из Quintic Linear Analysis. Гравитационная постоянная была принята равной 9,81, а измеренная масса шаров — 0,022 кг. В Приложении А показаны кинетическая и потенциальная энергия пяти шаров во время первого качания маятника. График 1 иллюстрирует табличные данные из Приложения A.
График показывает, что в начале замаха шар 1 имеет значение потенциальной энергии 0,005 Дж и значение кинетической энергии 0.0001. Когда мяч начинает опускаться по дуге, потенциальная энергия уменьшается, поскольку она преобразуется в кинетическую энергию. Это называется обратной зависимостью, когда одно значение увеличивается, другое уменьшается. Поскольку энергия не может быть создана или уничтожена, потенциальная энергия преобразуется в кинетическую энергию
График 1 также демонстрирует, что во время первого замаха общая энергия люльки остается постоянной на протяжении маха вниз шара 1 и подъема шара 5, демонстрируя сохранение энергии и передачу энергии шаров 11 через статические шары в шар 5. .График действительно демонстрирует уменьшение общей энергии системы на 3/4 кадра до контакта и на 3/4 кадра после контакта, это связано с ошибкой сглаживания данных. Если эксперимент продолжится, мы ожидаем увидеть такое же соотношение кинетической энергии и потенциальной энергии, хотя значения кинетического потенциала и полной энергии системы уменьшатся из-за потерь энергии из-за теплового звука и сил трения.
График 1: кинетическая энергия, потенциальная энергия и полная энергия системы во время качания 1
Номер рамы | Общая кинетическая энергия системы | Общая потенциальная энергия системы | Общая энергия системы |
2 | 0.0001 | 0,0053 | 0,0054 |
3 | 0,0002 | 0,0052 | 0,0054 |
4 | 0,0003 | 0,0051 | 0,0054 |
5 | 0,0006 | 0.0049 | 0,0054 |
6 | 0,0008 | 0,0046 | 0,0054 |
7 | 0,0012 | 0,0042 | 0,0054 |
8 | 0,0015 | 0,0038 | 0.0053 |
9 | 0,0019 | 0,0034 | 0,0053 |
10 | 0,0023 | 0,0030 | 0,0053 |
11 | 0,0027 | 0,0025 | 0,0053 |
12 | 0.0031 | 0,0021 | 0,0052 |
13 | 0,0035 | 0,0017 | 0,0052 |
14 | 0,0038 | 0,0013 | 0,0051 |
15 | 0,0038 | 0.0010 | 0,0049 |
16 | 0,0035 | 0,0008 | 0,0043 |
17 | 0,0030 | 0,0007 | 0,0037 |
18 | 0,0026 | 0,0007 | 0.0033 |
19 | 0,0026 | 0,0007 | 0,0033 |
20 | 0,0030 | 0,0008 | 0,0037 |
21 | 0,0034 | 0,0009 | 0,0043 |
22 | 0.0036 | 0,0012 | 0,0048 |
23 | 0,0035 | 0,0015 | 0,0050 |
24 | 0,0033 | 0,0019 | 0,0052 |
25 | 0,0029 | 0.0024 | 0,0053 |
26 | 0,0025 | 0,0028 | 0,0054 |
27 | 0,0021 | 0,0033 | 0,0054 |
28 | 0,0017 | 0,0037 | 0.0054 |
29 | 0,0013 | 0,0042 | 0,0055 |
30 | 0,0010 | 0,0045 | 0,0055 |
31 | 0,0007 | 0,0048 | 0,0055 |
32 | 0.0004 | 0,0051 | 0,0055 |
33 | 0,0002 | 0,0053 | 0,0055 |
34 | 0,0001 | 0,0054 | 0,0055 |
35 | 0,0000 | 0.0054 | 0,0055 |
36 | 0,0000 | 0,0055 | 0,0055 |
Исследования будущего
В будущих исследованиях следует выяснить, демонстрирует ли колыбель Ньютона законы импульса и сохранения энергии, если использовать следующие установки.
- Серия шаров разного размера, одинаковой массы.
- Серия шаров разной массы
- Маятник разной длины.
Загрузки
Письменный пример | Таблица данных Excel | Видео avi. файлы |
| ~ 0,5 МБ | ~ 0,6 МБ | Видео 1 ~ 1.0 МБ |
Модифицированная колыбель Ньютона, демонстрирующая механический импеданс
Обзор
Хотя классическое устройство, известное как «Колыбель Ньютона», часто можно встретить на офисных столах по всему миру, его практическое применение выходит за рамки успокаивающего воздействия на напряженного работника.В классе это устройство может использоваться педагогами для демонстрации принципов импульса и сохранения энергии. Обычно пользователь оттягивает одну из металлических сфер на желаемую высоту, прежде чем отпустить ее. Когда сфера возвращается в исходное положение, она ударяется о колыбель (ряд сфер), сохраняя и передавая энергию через группу, и заставляя противоположную сферу качаться вверх в соответствии с начальной высотой, на которой была выпущена исходная сфера.Классическая колыбель Ньютона полезна для демонстрации этих принципов, но не позволяет инструктору показать эффекты механического сопротивления.
Изобретение
Профессор физики и изобретатель из Университета Висконсина — Уайтуотер разработал модифицированную колыбель Ньютона, которая позволяет пользователю визуализировать и тестировать концепцию механического импеданса в дополнение к сохранению импульса и энергии. Традиционная версия колыбели Ньютона имеет колыбель из идентичных металлических сфер.В этом модифицированном и улучшенном устройстве пользователь может заменять эти сферы сферами различной массы и состава. Позволяя пользователю стратегически выровнять и создать уникальную подставку, они получают возможность визуализировать механическое сопротивление. Например, сфера с небольшой массой могла бы удариться о колыбель и поднять сферу большей массы с противоположной стороны, если бы сферы между ними сами имели градиент увеличения массы. Возможность смены сферы в любом месте подставки позволяет проводить исключительно большое количество возможных экспериментов и в целом приведет к более глубокому пониманию вышеупомянутых физических концепций, чего не обеспечивает традиционное устройство-подставка.


 Шарики должны выровняться как по горизонтали, так и при взгляде сверху.
Шарики должны выровняться как по горизонтали, так и при взгляде сверху.  Некоторые идеи для вопросов: какие материалы сферы лучше всего демонстрируют импульс (мрамор, шарикоподшипники, деревянные бусины, жевательные резинки)? Можете ли вы придать деревянным бусинам больше массы, чтобы они работали в этой демонстрации? Как? Насколько жесткой должна быть рама, чтобы проект работал? Влияет ли количество сфер на то, как это работает? Что произойдет, если у вас на линии будет больше сфер? Что будет, если у вас будет меньше?
Некоторые идеи для вопросов: какие материалы сферы лучше всего демонстрируют импульс (мрамор, шарикоподшипники, деревянные бусины, жевательные резинки)? Можете ли вы придать деревянным бусинам больше массы, чтобы они работали в этой демонстрации? Как? Насколько жесткой должна быть рама, чтобы проект работал? Влияет ли количество сфер на то, как это работает? Что произойдет, если у вас на линии будет больше сфер? Что будет, если у вас будет меньше? Обязательно записывайте каждый эксперимент и то, что происходит; это называется вашими данными.
Обязательно записывайте каждый эксперимент и то, что происходит; это называется вашими данными. Ваша гипотеза верна?
Ваша гипотеза верна? avi
avi
 м / с)
м / с) 472
472 33
33 88
88 84
84 022
022 022
022 м / с)
м / с) 441
441 000
000 52
52 02
02 46
46 022
022 022
022 286
286 18
18 556
556 92
92 577
577 30
30