Неметрические шкалы — Студопедия
Поделись с друзьями:
1.4.1 Шкала физической величины
Шкала физической величины (от латин. scala — лестница) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на основании результатов точных измерений.
Например, международная температурная шкала, состоящая из ряда реперных точек, значения которых приняты по соглашению между странами Метрической Конвенции и установлены на основании точных измерений, предназначена служить исходной основой для измерений температуры
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом. В теории измерений различают пять основных типов шкал измерений:
— неметрические шкалы: шкалы наименований (классификации) и шкалы порядка;
— метрические шкалы: шкалы интервалов, шкалы отношений, абсолютные шкалы.
Неметрическими шкалами называют условные шкалы физических величин, исходные значения которых выражены в условных единицах.
Шкалы наименований (классификации) используются для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета, марки автомобилей и т.п.
При большом числе классов используют иерархические шкалы наименований.
С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию — проверку их совпадения или несовпадения. По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа — критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам.
Примеры:
— системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение;
— цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета;
— многочисленные виды классификаций, которые существуют во многих разновидностях: например, с помощью диагностических средств классифицируют болезни, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т. д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
Номинальная шкала, используемая для классификации, называется шкалой классификации.
В шкале классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, – это отношение эквивалентности. Такие признаки удовлетворяют аксиомам тождества:
Либо А = В, либо А ≠ В;
Если А = В, то В = А;
Если А = В и В = С, то А = С.
Шкалы порядка (рангов) являются монотонно изменяющимися и позволяют установить отношение «больше – меньше» между величинами, характеризующими это свойство. Если для обозначения реперных точек используются цифры, то они называются баллами.
Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать, т.е. на шкале порядка не определены никакие математические операции.
В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего. Т.е. для любых чисел a, b и c таких, что a < b и b < c, справедливо соотношение a < c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Q i, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Q j. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Т.е. для любых чисел a, b и c таких, что a < b и b < c, справедливо соотношение a < c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Q i, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Q j. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко.
Пример — В образовательных учреждениях по шкале порядка, представленной в таблице 1.4, измеряются знания учащихся.
Таблица 1.4 – Сравнение российской и международной систем оценки знаний
| Российские оценки | ECTS | Смысловое содержание оценки |
| 5 | A | Отлично |
| 4 | B | Очень хорошо |
| C | Хорошо | |
| 3 | D | Удовлетворительно |
| E | Посредственно | |
| 2 | FX | Неудовлетворительно (с правом пересдачи) |
| * | F | Неудовлетворительно (без права пересдачи) |
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2 и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.
Упорядочение в шкале порядка может осуществляться по внешним признакам (нумерация) или по внутренним свойствам (ранжирование).
Примеры:
— нумерация мест в театрах, домов на улице, исследуемых образцов промышленных изделий и т.д.;
— ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов, представленная в таблице 1.5. В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.
Таблица 1.5 — Минералогическая шкала твёрдости
| Балл | Твёрдость |
| Меньше твёрдости талька | |
| Равна или больше твёрдости талька, но меньше твёрдости гипса | |
| Равна или больше твёрдости гипса, но меньше твёрдости извес ткового шпата | |
| Равна или больше твёрдости известкового шпата, но меньше твёрдости плавикового шпата | |
| Равна или больше твёрдости плавикового шпата, но меньше твёрдости апатита | |
| Равна или больше твёрдости апатита, но меньше твёрдости полевого шпата | |
| Равна или больше твёрдости полевого шпата, но меньше твёрдости кварца | |
| Равна или больше твёрдости кварца, но меньше твёрдости топаза | |
| Равна или больше твёрдости топаза, но меньше твёрдости корунда | |
| Равна или больше твёрдости корунда, но меньше твёрдости алмаза | |
| Равна твёрдости алмаза или больше её |
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным. Не все объекты можно подчинить отношению порядка. Например, нельзя сказать, что больше — круг или треугольник, но можно выделить в этих объектах общее свойство — площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
42 Использование в психологии шкал измерения (по с. Стивенсу)
Понятие
измерения в психологии. Особенности
психологических измерений.
Измерение
– приписывание числовых форм
объектам\событиям в соответствии с
определенными правилами. Это правило
устанавливает соответствие между
измеряемым свойством объекта и результатом
измерения признака.
Виды
измерений:
1
Нормативное
– результат испытуемого сравнивается
с результатом других людей (эталонной
группой лиц)
2
Критериальное
— результат испытуемого сравнивается
с каким-то критерием; определяется не
относительный, а абсолютный статус
3
Ипсативное
— результат испытуемого сравнивается
с его предыдущим уровнем
Проблема
измерения в психологии связана с:
-объектом
измерения (человеком)
—
методами измерения (тест)
—
исследователем, испытателем,
эксперементатором.
Измерения
в психологии — процедуры определения
количественной выраженности психологических
феноменов. В них применяются разнообразные
шкалы, содержащие некое множество
позиций, поставленных в некое соответствие
с психологическими элементами.
Разнообразные
виды измерения в теоретическом плане
формализуются с помощью понятий числового
представления и шкалы. Числовое
Числовое
представление —
это функция, гомоморфно отображающая
эмпирическую систему с отношениями в
числовую систему с отношениями.
Шкалирование.
Шкала
измерения – форма фиксации результатов
измерения с упорядочиванием их в
определенную числовую систему.
Шкала —
это множество чисел, отношения между
которыми отражают отношения между
объектами эмпирической системы. В
частности, шкалой можно назвать результаты
измерения, полученные определенной
системой вопросов, заданных испытуемому,
а также сам инструмент измерения (т. е.
систему вопросов, опросник, тест). Шкалы
разделяют по типу в соответствии с тем,
какие отношения они отражают, и, что
эквивалентно, теми допустимыми
(математическими) преобразованиями,
которые оставляют инвариантными
соответствующие отношения.
Классификация
шкал измерения (С. Стивенс).
А)неметрические
измерительные шкалы
Номинативная
шкала
(неметрическая), или шкала наименований —
это шкала, классифицирующая по названию
(лат. nomen — имя, название). В её основе
nomen — имя, название). В её основе
лежит процедура, обычно не ассоциируемая
с измерением. Пользуясь определённым
правилом, объекты группируются по
различным классам так, чтобы внутри
класса они были идентичны по измеряемому
свойству. Затем каждому объекту
присваивается соответствующее
обозначение.
Простейший
случай номинативной шкалы — дихотомическая
шкала,
состоящая всего лишь из двух ячеек,
например: «имеет братьев и сестер —
единственный ребенок в семье»; «иностранец
– соотечественник»; проголосовал «за»
— проголосовал «против» и т.п.
Признак,
который измеряется по дихотомической
шкале наименований, называется
альтернативным. Он может принимать
всего два значения. При этом исследователь
зачастую заинтересован в одном из них,
и тогда он говорит, что признак «проявился»,
если тот принял интересующее его
значение, и что признак «не проявился»
, если он принял противоположное значение.
Например: «Признак леворукости проявился
у 8 испытуемых из 20». В принципе номинативная
В принципе номинативная
шкала может состоять из ячеек «признак
проявился — признак не проявился».
Более
сложный вариант номинативной шкалы —
классификация из трех и более ячеек,
например: «экстрапунитивные
— интрапунитивные — импунитивные реакции»
или «выбор кандидатуры А — кандидатуры
Б -кандидатуры В — кандидатуры Г» или
«старший — средний — младший — единственный
ребенок в семье» и др.
Таким
образом, номинативная шкала позволяет
нам подсчитывать частоты встречаемости
разных «наименований», или значений
признака, и затем работать с этими
частотами с помощью математических
методов.
Единица
измерения, которой мы при этом оперируем
— количество наблюдений (испытуемых,
реакций, выборов и т. п.), или частота.
Точнее, единица измерения — это одно
наблюдение.
*
Объекты А и Б принадлежат разным классам,
но не известно насколько (определяется
есть или нет признак). шкала
наименований отражает отношения типа:
похож/не похож, тот/не тот, относится к
группе/не относится к группе
Примером
шкалы такого рода может служить
классификация испытуемых на мужчин и
женщин
Порядковая
шкала, или ранговая шкала —
это шкала, классифицирующая по принципу
«больше – меньше» (в соответствии с
возрастанием или убыванием значений
общего для этих объектов признака). Как
Как
следует из названия, измерение в этой
шкале предполагает приписывание объектам
чисел в зависимости от степени выраженности
измеряемого свойства. Если в шкале
наименований было безразлично, в каком
порядке мы расположим классификационные
ячейки, то в порядковой шкале они образуют
последовательность от ячейки «самое
малое значение» к ячейке «самое большое
значение» (или наоборот). Ячейки теперь
уместнее называть классами,
поскольку по отношению к классам
употребимы определения «низкий»,
«средний» и «высокий» класс (ранг),
или 1-й, 2-й, 3-й класс, и т.д.
Каждому
объекту приписывается число, которое
называется ранг,
а процесс измерения по этой шкале –
ранжирование.
В
порядковой шкале должно быть не менее
трех классов например «положительная
реакция — нейтральная реакция —
отрицательная реакция» или «подходит
для занятия вакантной должности —
подходит с оговорками — не подходит» и
т. п.
*
В порядковой шкале мы не знаем истинного
расстояния между классами а знаем лишь,
что они образуют последовательность.
Если объектам А и Б приписаны разные
ранги, то можно сказать, что они отличаются
в отношении измеряемого свойства и
можно определить какой объект в большей
степени обладает свойством, а какой в
меньшей.
От
классов легко перейти к числам, если мы
условимся считать, что низший класс
получает ранг 1, средний класс — ранг 2,
а высший класс — ранг 3, или наоборот. Чем
больше классов в шкале, тем больше у нас
возможностей для математической
обработки полученных данных и проверки
статистических гипотез.
Единица
измерения в шкале порядка — расстояние
в 1 класс или в 1 ранг, при этом расстояние
между классами и рангами может быть
разным (оно нам неизвестно).
При
ранжировании,
следует иметь в виду два обстоятельства:
Установите
для себя и запомните порядок ранжирования.
Вы можете ранжировать испытуемых по их
«месту в группе»: ранг 1 присваивается
тому, у которого наименьшая выраженность
признака, и далее – увеличение ранга
по мере увеличения признака. Или можно
Или можно
ранг 1 присваивать тому, у которого 1-е
место по выраженности данного признака
(например, «самый быстрый»). Строгих
правил выбора здесь нет, но важно помнить,
в каком направлении проводилось
ранжирование (возрастание\убывание).
Соблюдайте
правило ранжирования для связанных
рангов, когда двое и более испытуемых
имеют одинаковую выраженность измеряемого
свойства. В этом случае таким испытуемым
присваиваются один и тот же, средний
ранг. Например, если вы ранжируете
испытуемых по «месту в группе» и двое
имеют одинаковые самые высокие исходные
оценки, то обоим присваивается средний
ранг 1,5: (1+2)/2 = 1,5. Следующему за этой парой
испытуемому присваивается ранг 3, и т.д.
Это правило основано на соглашении
соблюдения одинаковой суммы рангов для
связанных и несвязанных рангов. В
соответствии с этим правилом сумма всех
присвоенных рангов для группы численностью
N должна равняться N(N+1)/2, вне зависимости
от наличия или отсутствия связей в
рангах.
Пример
метод экспертных оценок. К
К
примеру, когда человека просят
проранжировать цвета по предпочтению,
от самого приятного, до самого неприятного.
В этом случае, мы точно можем сказать,
что один цвет приятнее другого, но о
единицах измерения мы не можем даже
предположить, т.к. человек ранжировал
цвета не на основе каких-либо единиц
измерения, а основываясь на собственных
чувствах. То же самое происходит в тесте
Рокича, по результатам которого мы так
же не знаем на сколько единиц одна
ценность выше (больше) другой. Т.е., в
отличие от соревнований, мы даже не
имеем возможности узнать точные баллы
различий.
Б)метрические
измерительные шкалы.
Интервальная
шкала
–
произвольно выбирается нулевая точка
(не значит, что свойство полностью
отсутствует) и единица измерения; это
шкала, классифицирующая по принципу
«больше на определенное количество
единиц — меньше на определенное количество
единиц». Каждое из возможных значений
признака отстоит от другого на равном
расстоянии. Шкала интервалов определяет
Шкала интервалов определяет
величину различий между объектами в
проявлении свойства. Она дополняет идею
ранжирования принципом равных интервалов
между ранжируемыми явлениями.
*
Если объектам А и Б приписаны разные
интервальные оценки, то можно сказать
насколько эти объекты отличаются.
Наиболее
распространенный пример использования
интервальной шкалы — психологические
тесты личности, установок и способностей.
Например, результаты теста интеллекта
обычно представляются подобным образом.
Некто, имеющий IQ 120, предполагается более
умным (предположим, что IQ определяет
умственные способности), чем тот, чей
IQ равен 110.
Шкала
равных отношений или абсолютная шкала –
характеризуется тем, что нулевая точка
зафиксирована и обозначает полное
отсутствие признака; это шкала,
классифицирующая объекты или субъектов
пропорционально степени выраженности
измеряемого свойства.
По
отношению к показателям частот возможно
применять все арифметические операции:
сложение, вычитание, деление и умножение.
Единица измерения в этой шкале отношений
— 1 наблюдение, 1 выбор, 1 реакция и т. п.
Мы вернулись к тому, с чего начали: к
универсальной шкале измерения в частотах
встречаемости того или иного значения
признака и к единице измерения, которая
представляет собой 1 наблюдение.
*
Если объектам А и Б разные показатели,
то можно сказать насколько и во сколько
раз они отличаются.
Пример
любые признаки, значения которых
получается при счете (количество выборов,
ошибок)
1. Дихотомическая
классификация часто
рассматривается как вариант шкалы
наименований. Это верно, за исключением
одного случая, когда мы измеряем свойство,
имеющее всего лишь два уровня выраженности:
«есть—нет», так называемое «точечное»
свойство. Примеров таких свойств много:
наличие или отсутствие у испытуемого
какой-либо наследственной болезни
(дальтонизм, болезнь Дауна, гемофилия
и др.), абсолютного слуха и др. В этом
случае исследователь имеет право
проводить «оцифровку» данных, присваивая
каждому из типов цифру «1» или «0», и
работать с ними как со значениями шкалы
интервалов.
Некоторые мысли о метрических и неметрических данных в исследованиях рынка
Перейти к основному содержанию
Рэй Пойнтер
Рэй Пойнтер
На пересечении работы, развлечений и открытий
Опубликовано 18 августа 2017 г.
+ Подписаться
Вот некоторые мои мысли о метрических и неметрических данных, они совпадают с вашими? Что бы вы добавили, изменили, спросили?
Метрические данные
Метрические данные — это то, что большинство людей имеет в виду, когда говорят о «числах», типах чисел, которые мы собираем, когда что-то измеряем. Сколько лет кому-то является примером метрических данных, так же как и рейтинговая шкала, где кто-то указывает, насколько вероятно, что он порекомендует продукт или услугу по шкале от 0 до 10.
Сколько лет кому-то является примером метрических данных, так же как и рейтинговая шкала, где кто-то указывает, насколько вероятно, что он порекомендует продукт или услугу по шкале от 0 до 10.
Метрические данные можно разделить на подкатегории, и две ключевые из них — шкалы отношений и шкалы интервалов.
Шкала отношений
Шкала отношений — это термин, который мы используем, когда есть «настоящий» ноль, т. е. 0 означает полное отсутствие того, что измеряется. Например, вопрос «Сколько раз вы ели карри в этом месяце?» дает данные по шкале соотношения. Кто-то, кто ел карри 8 раз за последний месяц, съел его в два раза больше, чем тот, кто ел карри 4 раза. Только шкалы отношений позволяют нам сказать, что 8 в два раза больше, чем 4, или что увеличение от 4 до 6 составляет увеличение на 50%.
Интервальная шкала
Интервальная шкала описывает шкалу, в которой единицы шкалы измеряют непротиворечивую концепцию. В интервальной шкале разрыв между 2 и 4 такой же, как разрыв между 6 и 8. Однако интервальная продажа не имеет «настоящего» нуля.
Однако интервальная продажа не имеет «настоящего» нуля.
И Фаренгейты, и Цельсия являются примерами шкал интервалов. Если температура изменяется от 50°F до 70°F, изменение составляет 20°F; если температура изменится с 80°F на 100°F, это также будет изменением на 20°F. Однако 100°F не в два раза горячее, чем 50°F, потому что 0°F не означает, что вообще нет тепла.
В маркетинговых исследованиях многие шкалы, которые мы используем, такие как пятибалльная шкала «Согласен-Не согласен», дают данные шкалы интервалов. Например, если шкала использует значения от 1 для «Совершенно не согласен» до 5 для «Совершенно согласен», то изменение среднего значения с 2 до 3 не означает увеличение на 50%, а среднее значение 4 не в два раза превышает среднее значение 2.
Целочисленная шкала
Целочисленная шкала относится к метрической шкале (интервал или отношение), в которой используются только целые числа (числа без десятичных значений). Количество людей в классе – это целочисленная шкала отношений, дробей людей нет. Пятибалльная шкала «Согласен-Не согласен» представляет собой целочисленную интервальную шкалу.
Пятибалльная шкала «Согласен-Не согласен» представляет собой целочисленную интервальную шкалу.
Кардинальные числа
Термин кардинальное число часто используется по сравнению с порядковым (где порядковый номер относится к ранжированным данным). Кардинальные числа относятся к подсчету вещей, таких как количество детей, количество дней и т. д. Кардинальные числа — это либо 0, либо положительное целое число. В контексте маркетинговых исследований термина «кардинальный», вероятно, следует избегать; такие термины, как интервал или шкала отношений, обычно более полезны.
Почему это важно?
Многие статистические методы, которые мы используем в исследованиях рынка, включая среднее значение и стандартное отклонение, «работают» только с метрическими данными. Термин «работа» в этом контексте выражает вероятность того, что мы получим надежные и осмысленные ответы, если воспользуемся этими методами.
Неметрические данные
Неметрические данные относятся ко всем структурированным данным, используемым исследователями рынка, которые не являются метрическими данными. Например, неметрические данные включают ранжированную информацию (называемую порядковой) и информацию, не имеющую линейной закономерности (называемую номинальной или категориальной).
Например, неметрические данные включают ранжированную информацию (называемую порядковой) и информацию, не имеющую линейной закономерности (называемую номинальной или категориальной).
Порядковые данные
Примером порядковых данных может быть вопрос, в котором людям показывают четыре праздника и просят ранжировать их от первого до последнего выбора. Другое название порядковых данных — ранжированные данные.
Иногда порядковые данные преобразуются в метрические данные путем преобразования данных. Автомобильный чемпионат Формулы-1 демонстрирует один из примеров такого процесса трансформации. В 2017 году очки начисляются за автомобили, занявшие первые десять мест в каждой гонке, победитель (т.е. 1-й) получает 25 баллов, 2-й — 18 баллов, 3-й — 15 баллов, вплоть до 10-го автомобиля, получающего 1 очко. Эти баллы накапливаются в течение сезона и составляют целочисленную шкалу.
Номинальные или категориальные данные
Простая номинальная шкала может быть «Вы? Мужчина или женщина?», чуть более сложным может быть что-то вроде «В каком регионе вы живете? Азия, Австралазия, Европа, Северная Америка, Южная Америка, Другое».
В исследованиях рынка категориальные данные могут быть представлены в форме взаимоисключающих категорий, таких как «Что из следующего было бы вашим первым выбором? Говядина, свинина, курица, ничего из этого». Однако он также может разрешать множественный выбор, например: «Что из следующего вы едите хотя бы раз в месяц? Говядина, свинина, курица, ничего из этого».
Решение о том, являются ли некоторые шкалы категориальными или порядковыми, иногда может быть весьма субъективным. Например, на вопрос «Какой самый высокий уровень образования вы получили?» за которым следует ряд вариантов от конкретных лет в средней школе до уровней последипломного образования, может считаться категориальным (т. возможно, «Some High School» — это другой конец.0003
Дихотомические данные
Категориальные данные только с двумя вариантами (например, гендерный вопрос только с вариантами «Мужской» и «Женский») также можно рассматривать как переменную особого типа, называемую дихотомической переменной. Переменная такого рода может быть закодирована как 1 и 0 (например, 1, если кто-то является женщиной, и 0, если это мужчина), что делает переменную подходящей для ряда статистических методов, таких как логистическая регрессия. Данные выбора (в отличие от ранжирования или рейтинга) имеют тенденцию давать дихотомические данные, а методы анализа, как правило, основаны на методах, основанных на том, что все данные равны 1 или 0. Это область роста с точки зрения анализа в исследованиях рынка.
Переменная такого рода может быть закодирована как 1 и 0 (например, 1, если кто-то является женщиной, и 0, если это мужчина), что делает переменную подходящей для ряда статистических методов, таких как логистическая регрессия. Данные выбора (в отличие от ранжирования или рейтинга) имеют тенденцию давать дихотомические данные, а методы анализа, как правило, основаны на методах, основанных на том, что все данные равны 1 или 0. Это область роста с точки зрения анализа в исследованиях рынка.
Почему это важно?
С неметрическими данными мы не можем использовать такие инструменты, как среднее значение, стандартное отклонение, тесты z или факторный анализ. Мы используем семейство статистических данных, называемых непараметрическими статистическими данными, такими как количество, проценты, хи-квадрат, мода и медиана. В случае дихотомических переменных у нас также есть возможность использовать логистические методы.
Инфляция и выводы
17 августа 2022 г.

Новое мышление в качественных исследованиях
6 июня 2022 г.
Участник кризиса 2022 г.
6 апр. 2022 г.
Что вы думаете о новостных рассылках LinkedIn? (И должен ли я производить один?)
28 марта 2022 г.
Уроки из Музея искусств и ремесел в Париже
27 марта 2022 г.

Хорошие и плохие бассейны – Сравнение хороших и плохих
5 фев. 2019 г.
Что такое семиотика и как она используется?
17 июля 2018 г.
Структура знаний о проектах
10 июля 2018 г.
Исследователи должны знать о проблемах с данными наблюдений
18 мая 2018 г.

Какая визуализация данных вам действительно нужна?
27 апр. 2018 г.
Увидеть все
Другие также смотрели
Исследуйте темы
Шкалы измерения: номинальная, порядковая, интервальная, отношение
Имеется четыре шкалы измерения: Номинальная, Порядковая, Интервальная, Относительная.
Они учитываются в рамках качественных и количественных данных как:
Качественные данные:
- Номинальная шкала :
В этой шкале категории являются номинальными именами (отсюда «номинальные»). Между категориями нет внутреннего порядка. Проще говоря, нельзя сказать, что какая-то конкретная категория выше/лучше другой.
Между категориями нет внутреннего порядка. Проще говоря, нельзя сказать, что какая-то конкретная категория выше/лучше другой.
Примеры :
- Пол (мужской/женский) :- Нельзя сказать, что мужчины лучше женщин, или наоборот.
- Группы крови (A/B/O/AB) :- Нельзя сказать, например, что группа A превосходит группу O.
- Религия (индуистская/мусульманская/христианская/буддистская и т. д. ): — Здесь категории также нельзя расположить в логическом порядке. Каждая категория может рассматриваться только как равная другой.
- Порядковая шкала:
Различные категории можно логически расположить в осмысленном порядке. Однако разница между категориями не является «значимой».
Примеры :
- Ранги (1-й/2-й/3-й и т. д.) : Ранги можно без труда расположить в порядке возрастания или убывания.
 Однако разница между рангами неодинакова — разница между 1-м и 2-м рангами может составлять 20 единиц, а между 2-м и 3-м рангами может быть 3 единицы. Кроме того, нельзя сказать, что 1-й ранг в х раз лучше 2-го или 3-го ранга чисто на основании рангов.
Однако разница между рангами неодинакова — разница между 1-м и 2-м рангами может составлять 20 единиц, а между 2-м и 3-м рангами может быть 3 единицы. Кроме того, нельзя сказать, что 1-й ранг в х раз лучше 2-го или 3-го ранга чисто на основании рангов. - Ранги (хорошее/лучшее/лучшее), (нет боли/слабая боль/умеренная боль/сильная боль) : Здесь тоже возможно осмысленное расположение (упорядочение), но разница между категориями субъективна и неоднородна . «Лучший» не обязательно в три раза лучше, чем «Хороший»; или в два раза лучше, чем «Лучше».
- Шкала Лайкерта (Совершенно не согласен / Не согласен / Нейтрально / Согласен / Полностью согласен) : Порядок может быть гибким — порядок можно легко изменить, не влияя на интерпретацию — (Совершенно согласен/Согласен/Нейтрально/Не согласен/Совершенно не согласен). Опять же, разница между категориями неравномерна.
Количественные данные :
- Интервальная шкала :
Значения (не категории) могут быть упорядочены и иметь значимую разницу, но удвоение не имеет смысла. Это связано с отсутствием «абсолютного нуля».
Это связано с отсутствием «абсолютного нуля».
Пример : Шкала Цельсия : Разница между 40°C и 50°C такая же, как между 20°C и 30°C (значимая разница = равноудаленная). Кроме того, 50 С жарче, чем 40 С (на порядок). Тем не менее, 20 C не в два раза горячее, чем 40 C, и наоборот (удвоение не имеет смысла).
Значимая разница : В шкале Цельсия разница между всеми единицами одинакова в любой точке шкалы – разница между 49°C и 50°C такая же, как разница между любыми двумя последовательными значениями на шкале ( 1 единица). [Таким образом, (2-1)= (23-22)= (40-39)=(99-98)= 1].
- Шкала отношений :
Значения могут быть упорядочены, имеют смысловую разницу, и удвоение также имеет смысл. Есть «абсолютный ноль».
Примеры :
- Шкала Кельвина : 100 К вдвое горячее, чем 50 К; разница между значениями имеет смысл и может быть упорядочена.

- Вес : 100 кг в два раза тяжелее 50 кг; разница между 45 кг и 55 кг такая же, как между 105 кг и 100 кг; значения могут быть расположены в порядке (по возрастанию/убыванию).
- Высота : 100 см выше 50 см; эта разница такая же, как между 150 см и 100 см или 200 см и 150 см; 100 см вдвое больше 50 см; значения могут быть расположены определенным образом (по возрастанию/убыванию).
Кроме того, количественные данные также могут быть классифицированы как дискретные или непрерывные .
Дискретный :
Значения могут быть только конкретными числами. Дроби бессмысленны . В некоторых ситуациях математические функции также невозможны.
Примеры :
- Количество детей : 1, 2, 3 и т. д. возможно, но 1,5 ребенка не имеет смысла.
- Количество голосов : значимы 100, 102 и т.
 д., а не 110,2 голоса.
д., а не 110,2 голоса. - Номер водительского удостоверения/ Идентификационный номер избирателя/ Номер персонального номера : Число является дискретным значением, но его нельзя использовать для сложения или вычитания и т. д.
Непрерывный :
Любое числовое значение (включая дроби) возможно и имеет смысл.
Примеры :
- Вес : 1 кг, 1,0 кг, 1000 кг, 1,00001 кг — все значения имеют смысл. Уровень точности зависит от оборудования, используемого для измерения веса.
- Высота : 10 м, 10,03 м, 10,0005 м имеют значение.
- Температура : 100,0 F, 102,5 F, 99,8 F имеют смысл.
- Время : 1,023 с, 1,00002 с, имеют смысл. Математические функции (сложение, вычитание и т. д. имеют смысл).
Большинство числовых данных, которые мы используем, являются непрерывными. Как вы, возможно, уже заметили, шкала отношений часто включает непрерывные данные [температура является исключением, если только не используется шкала Кельвина].
Как вы, возможно, уже заметили, шкала отношений часто включает непрерывные данные [температура является исключением, если только не используется шкала Кельвина].
.
Нажмите доступ 03a_continuous_descriptive.slides.pdf
Нравится:
Нравится Загрузка…
Эта запись была опубликована в Биостатистика и помечена как Непрерывная, Дискретная, Интервальная, Номинальная, Порядковая, Отношение, Шкалы измерения автором drroopesh.
Поиск:
Последние сообщения
- Что делать?
- Ваша диета полезна для сердца? Сравните с рекомендациями Американской кардиологической ассоциации.
- Всемирная неделя иммунизации (24–30 апреля 2023 г.): наверстать упущенное
- Всемирный день борьбы с малярией (25 апреля 2023 г.): «Время поставить нулевой уровень малярии: инвестировать, внедрять инновации, внедрять»
- Всемирный день болезни Шагаса (14 апреля 2023 г.
 ): время интегрировать болезнь Шагаса в систему первичной медико-санитарной помощи
): время интегрировать болезнь Шагаса в систему первичной медико-санитарной помощи
Архивы
Архивы
Выберите месяц май 2023 г. (2) апрель 2023 г. (4) март 2023 г. (5) февраль 2023 г. (4) январь 2023 г. (4) декабрь 2022 г. (5) ноябрь 2022 г. (4) октябрь 2022 г. (5) сентябрь 2022 г. (4) август 2022 г. ( 4) июль 2022 г. (5) июнь 2022 г. (4) май 2022 г. (5) апрель 2022 г. (4) март 2022 г. (5) февраль 2022 г. (4) январь 2022 г. (4) декабрь 2021 г. (5) ноябрь 2021 г. (4) октябрь 2021 г. ( 5) сентябрь 2021 г. (4) август 2021 г. (5) июль 2021 г. (4) июнь 2021 г. (5) май 2021 г. (4) апрель 2021 г. (4) март 2021 г. (5) февраль 2021 г. (3) январь 2021 г. (6) декабрь 2020 г. ( 5) ноябрь 2020 г. (4) октябрь 2020 г. (4) сентябрь 2020 г. (5) август 2020 г. (4) июль 2020 г. (5) июнь 2020 г. (5) май 2020 г. (5) апрель 2020 г. (6) март 2020 г. (6) февраль 2020 г. ( 4) январь 2020 г. (6) декабрь 2019 г.(4) ноябрь 2019 г. (5) октябрь 2019 г. (7) сентябрь 2019 г. (6) август 2019 г. (5) июль 2019 г. (5) июнь 2019 г. (5) май 2019 г. (7) апрель 2019 г. (6) март 2019 г. (8) февраль 2019 г. (6) январь 2019 г. (5) декабрь 2018 г. (8) ноябрь 2018 г. (8) октябрь 2018 г. (5) сентябрь 2018 г. (5) август 2018 г. (3) июль 2018 г. (4) июнь 2018 г. (7) май 2018 г. (10) апрель 2018 г. (6) март 2018 г. (5) февраль 2018 г. (4) январь 2018 г. (5) декабрь 2017 г. (8) ноябрь 2017 г. (7) октябрь 2017 г. (6) сентябрь 2017 г. (6) август 2017 г. (3) июль 2017 г. (6) июнь 2017 г. (5) май 2017 г. (8) апрель 2017 г. (9)) Март 2017 г. (7) Февраль 2017 г. (9) Январь 2017 г. (7) Декабрь 2016 г. (9) Ноябрь 2016 г. (6) Октябрь 2016 г. (10) Сентябрь 2016 г. (10) Август 2016 г. (5) Июль 2016 г. (13) Июнь 2016 г. (11) ) Май 2016 г. (12) Апрель 2016 г. (6) Март 2016 г. (7) Февраль 2016 г. (12) Январь 2016 г. (5) Декабрь 2015 г. (8) Ноябрь 2015 г. (15) Октябрь 2015 г. (11) Сентябрь 2015 г. (8) Август 2015 г. (7) ) июль 2015 г. (12) июнь 2015 г. (8) май 2015 г. (8) апрель 2015 г. (5) март 2015 г. (9) февраль 2015 г. (3) январь 2015 г.
(5) июнь 2019 г. (5) май 2019 г. (7) апрель 2019 г. (6) март 2019 г. (8) февраль 2019 г. (6) январь 2019 г. (5) декабрь 2018 г. (8) ноябрь 2018 г. (8) октябрь 2018 г. (5) сентябрь 2018 г. (5) август 2018 г. (3) июль 2018 г. (4) июнь 2018 г. (7) май 2018 г. (10) апрель 2018 г. (6) март 2018 г. (5) февраль 2018 г. (4) январь 2018 г. (5) декабрь 2017 г. (8) ноябрь 2017 г. (7) октябрь 2017 г. (6) сентябрь 2017 г. (6) август 2017 г. (3) июль 2017 г. (6) июнь 2017 г. (5) май 2017 г. (8) апрель 2017 г. (9)) Март 2017 г. (7) Февраль 2017 г. (9) Январь 2017 г. (7) Декабрь 2016 г. (9) Ноябрь 2016 г. (6) Октябрь 2016 г. (10) Сентябрь 2016 г. (10) Август 2016 г. (5) Июль 2016 г. (13) Июнь 2016 г. (11) ) Май 2016 г. (12) Апрель 2016 г. (6) Март 2016 г. (7) Февраль 2016 г. (12) Январь 2016 г. (5) Декабрь 2015 г. (8) Ноябрь 2015 г. (15) Октябрь 2015 г. (11) Сентябрь 2015 г. (8) Август 2015 г. (7) ) июль 2015 г. (12) июнь 2015 г. (8) май 2015 г. (8) апрель 2015 г. (5) март 2015 г. (9) февраль 2015 г. (3) январь 2015 г. (4) декабрь 2014 г. (5) ноябрь 2014 г. (6) октябрь 2014 г. (11) ) Сентябрь 2014 г. (10) Август 2014 г. (4) Июль 2014 г. (3) Июнь 2014 г. (7) Май 2014 г. (10) Апрель 2014 г. (13) Март 2014 г. (8) Февраль 2014 г. (11) Январь 2014 г. (8) Декабрь 2013 г. (8) ) Ноябрь 2013 г. (2) Октябрь 2013 г. (6) Сентябрь 2013 г. (4) Август 2013 г. (22) Июль 2013 г. (9)Июнь 2013 г. (3) апреля 2013 г. (2) января 2013 г. (5) декабрь 2012 г. (12) ноябрь 2012 г. (2)
(4) декабрь 2014 г. (5) ноябрь 2014 г. (6) октябрь 2014 г. (11) ) Сентябрь 2014 г. (10) Август 2014 г. (4) Июль 2014 г. (3) Июнь 2014 г. (7) Май 2014 г. (10) Апрель 2014 г. (13) Март 2014 г. (8) Февраль 2014 г. (11) Январь 2014 г. (8) Декабрь 2013 г. (8) ) Ноябрь 2013 г. (2) Октябрь 2013 г. (6) Сентябрь 2013 г. (4) Август 2013 г. (22) Июль 2013 г. (9)Июнь 2013 г. (3) апреля 2013 г. (2) января 2013 г. (5) декабрь 2012 г. (12) ноябрь 2012 г. (2)
Повестка дня антимикробной устойчивость Здоровье матери и ребенка Медицинское образование Психическое здоровье Психические карты Неинфекционные заболевания Уведомление о неинфекционных заболеваниях Питание Последипломное образование Профилактика бедности Первичная медико-санитарная помощь Методология исследований в области общественного здравоохранения Без категорий Насилие ВОЗ Всемирная организация здравоохранения (ВОЗ)
Этот сайт посетили более 2 миллионов раз
- 2 181 236 посещений
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.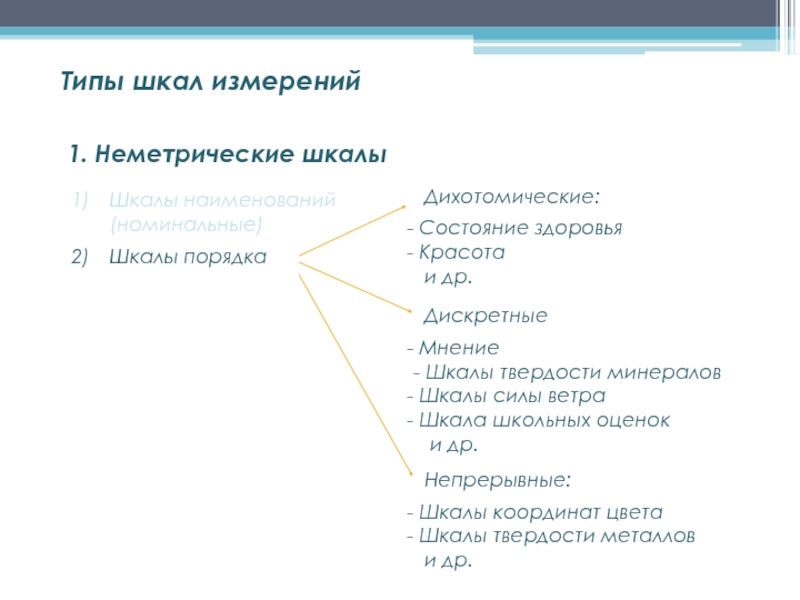




 Однако разница между рангами неодинакова — разница между 1-м и 2-м рангами может составлять 20 единиц, а между 2-м и 3-м рангами может быть 3 единицы. Кроме того, нельзя сказать, что 1-й ранг в х раз лучше 2-го или 3-го ранга чисто на основании рангов.
Однако разница между рангами неодинакова — разница между 1-м и 2-м рангами может составлять 20 единиц, а между 2-м и 3-м рангами может быть 3 единицы. Кроме того, нельзя сказать, что 1-й ранг в х раз лучше 2-го или 3-го ранга чисто на основании рангов.
 д., а не 110,2 голоса.
д., а не 110,2 голоса. ): время интегрировать болезнь Шагаса в систему первичной медико-санитарной помощи
): время интегрировать болезнь Шагаса в систему первичной медико-санитарной помощи