Шары ньютона принцип действия: Колыбель Ньютона »

Шары Ньютона – отличный сувенир для снятия стресса

По данным опроса World Health Organisation (Всемирной организации здравоохранения), практически каждый четвертый офисный работник имеет не менее четырех признаков депрессии. По-настоящему увлечены работой только 14% и всего лишь 12% выделяются своим оптимистическим настроем. Поэтому всем нам нужно почаще расслабляться. Помнить о необходимости отдыха на работе помогают различные антистрессы. Наиболее популярный из них – это маятник «шары Ньютона».

Преимущества антистресса

Снимать нервное напряжение на рабочем месте можно по-разному. Кто-то выбегает через каждые полчаса на перекур, кто-то часто пьет чай или кофе, а кто-то организует свое место по правилам фен-шуй и ставит на столе шары Ньютона. Сувенир этот не только позволяет отстраниться от того, что попросту невозможно контролировать, но и отлично украшает рабочее место, создавая атмосферу гармонии и порядка. Если разместить его на углу стола, то он будет являться своеобразным напоминанием о необходимости периодического отключения сознания от ежедневной рутины, а также помогать при медитации.

Что представляют собой шары Ньютона и кто их изобрел?

Данный антистресс представляет собой небольшую настольную кинетическую скульптуру в виде подставки с двумя металлическими опорами, на которых подвешено пять металлических шариков. Шары Ньютона демонстрируют и напоминают о великом законе сохранения энергии, философские предпосылки к открытию которого были заложены еще античными мудрецами. Изобрел этот сувенир не кто иной, как английский скульптур Саймон Преббл. Однажды в 1967 году, проводя опыты в своей мастерской, он вспомнил о законах Ньютона и решил создать очень необычную, эффектную и яркую модель, которая бы иллюстрировала принцип сохранения энергии и вместе с тем снимала бы усталость и стресс во время работы, тем самым способствуя душевному спокойствию человека.

Как действуют шары Ньютона?

Для того чтобы увидеть, как этот сувенир работает, достаточно взять один из крайних шариков, отвести его в сторону, а затем отпустить. После того как он ударится об своего соседа, с противоположной стороны произойдет зеркальное отображение данного движения, причем в том же ритме и с той же скоростью. Шарики посередине остаются неподвижными, а крайние будут колебаться до тех пор, пока силы упругости и трения не приведут к медленной остановке движения. Ритмичность движения и звуков как раз и создает эффект расслабления и стимулирует медитацию человека. Как долго будут двигаться шары Ньютона? Продолжительность работы такого оригинального подарка напрямую зависит от веса и размера шариков: чем больше их диаметр и чем они тяжелее, тем дольше будет длиться данный процесс, и наоборот.

В наше время, когда события в жизни происходят с сумасшедшей быстротой, шары Ньютона — это реальный способ отвлечься на время от суеты и окунуться в счастье беззаботности и покоя! Медитативное постукивание завораживающих взор шаров поможет не только сконцентрироваться на важной идее, но и просто расслабиться после какого-то напряженного дела на работе. Дополнительным их плюсом является то, что они не надоедают. Со временем этот сувенир остановится сам собой, а настроение незаметно изменится в лучшую сторону.

Сувенир-антистресс — Шары Ньютона, 9,5 см — Страна-изготовитель: Китай; «Полезный подарок для занятого человека! Сувенир-антистресс

372 р.

Купить

Страна-изготовитель: Китай; «Полезный подарок для занятого человека! Сувенир-антистресс — Шары Ньютона, 9,5 см; Принцип действия очень простой. Нужно отвести рукой и отпустить один из крайних шариков.

Доставка: По всей России
Качество: Высокое качество
Проверка товара перед отправкой:: Да
Рейтинг товара: ★★★★★
Скорость доставки: Быстрая (1-14 дней)
Страна-изготовитель: Китай «Полезный подарок для занятого человека! Сувенир-антистресс — Шары Ньютона, 9,5 см Принцип действия очень простой. Нужно отвести рукой и отпустить один из крайних шариков. Блестящие аксессуары придут в движение. Их медитативное постукивание позволит вам расслабиться и отвлечься или же наоборот, сосредоточиться и настроиться на рабочий лад! Действие инерционного маятника завораживает! Технические характеристики Материал: металл, пластик; Размеры: 9,5 х 7,5 х 8,8 см. VDomo — интернет-магазин полезных товаров для кухни и дома, каждый из которых делает жизнь чуточку приятнее! Мы отобрали для вас самое интересное, самое выгодное. Товары, которые представлены в нашем интернет-магазине имеют все необходимые документы для продажи в России. Мы продаем только те товары, которые есть на складе. Если вы видите товар на сайте, значит он есть в наличии. В нашей компании очень дружный коллектив, который сделает все, чтобы ваш заказ был оперативно обработан и доставлен. Вы ничем не рискуете! Мы не требуем предоплату за заказы. Вы можете оплатить свои покупки в момент получения – курьеру в крупных городах или на почте – по всей России. Заказывайте с уверенностью – вы в надежной компании! Мы гарантируем: Безопасность Никаких рисков! Мы гарантируем безопасность сделки – вы ничем не рискуете. Оплата осуществляется при получении в наших офисах, при получении в пунктах выдачи заказа, при получении на Почте или курьеру на руки при курьерской доставке. Или на сайте банковской картой, электронными деньгами или по квитанции в банк. Возврат денег. Если по любой причине вы недовольны покупкой, товар можно обменять или вернуть и получить назад деньги. Чтобы обменять или вернуть товар клиенту необходимо обратиться в наш контакт-центр по телефону или через контактную форму. Все способы связи описаны на странице «Контакты». Защита прав потребителей. Мы действуем в соответствии с Законом о защите прав потребителей, поэтому Вы можете быть уверены, что если Вас по каким-то причинам не устроит купленный товар, то Вы можете отказаться от него и получить уплаченные деньги назад. Гарантия качества. Все товары проходят проверку дважды: после прибытия на склад и непосредственно перед отправкой. Мы гарантируем качество наших товаров. Все товары мы получаем от проверенных поставщиков. Успейте купить Сувенир-антистресс — Шары Ньютона, 9,5 см со скидкой!

ньютоновская механика — колыбель Ньютона

спросил
11 лет, 9 месяцев назад

Изменено
5 лет, 2 месяца назад

Просмотрено
26 тысяч раз

$\begingroup$

Почему, когда в колыбели Ньютона выбрасывают 2 мяча, два мяча на противоположной стороне отскакивают примерно с той же скоростью, что и первая пара, а не один мяч с большей скоростью или 3 мяча с меньшей скоростью?

• ньютоновская механика
• сохранение энергии
• импульс
• законы сохранения
• столкновение

$\endgroup$

2

$\begingroup$

Вопреки тому, что утверждается во многих учебниках, закон сохранения энергии-импульса сам по себе не может объяснить поведение колыбели Ньютона. Для N шаров у нас есть два уравнения и N конечных скоростей для расчета. Следовательно, законы сохранения могут работать только для N = 2. Это означает, что если мы хотим дать объяснение поведения колыбели на основе законов сохранения, мы должны разделить столкновение N-шариков на последовательность столкновений двух шаров, как это делается в некоторых ответах на вопрос.

Проблема с этим подходом заключается в том, что он предполагает, что изначально шары не касаются друг друга, что не так в большинстве колыбелей. Можно возразить, что на самом деле не имеет значения, что шары первоначально соприкасаются, важно только то, что время столкновения (время, в течение которого импульс передается от одного шара к другому) намного меньше, чем время, необходимое для механического возмущения. пересечь один мяч. Однако типичное время столкновения составляет порядка 0,1 мс, что намного больше, чем время распространения, равное примерно 0,01 мс. В таких условиях следует ожидать, что распространение волны по шариковой цепи будет играть существенную роль в динамике люльки.

Есть красивая бумага,

Ф. Херрманн и П. Шмельцле. Простое объяснение известного эксперимента со столкновением. утра. Дж. Физ. 49 , выпуск 8, стр. 761 (1981). дои: 10.1119/1.12407. Версия в открытом доступе на веб-сайте Ф. Херрманна Karlsruher Physikkurs.

, показывающий, что распространение волны вдоль линии мяча должно быть бездисперсионным, если мы хотим найти одинаковое количество входящих и вылетающих мячей. Авторы также представляют интересную картину того, как система решает, сколько шаров она собирается отправить. По сути, первый удар производит два волновых импульса, движущихся в противоположных направлениях вдоль линии мяча. Импульсы отражаются на концах линии и снова встречаются в точке разрыва цепочки шариков. Легко видеть, что эта точка разрыва симметрична (относительно середины линии) точке удара, что объясняет, почему количество вылетающих шаров равно количеству входящих.

$\endgroup$

5

$\begingroup$

Одновременно сохраняет энергию и импульс при столкновении.

По замыслу, когда шары сталкиваются, нити, которые их удерживают, располагаются вертикально (при условии, что шары раскачиваются только с одной стороны). Это означает, что на шары не действуют горизонтальные силы от струны, поэтому линейный импульс в направлении качания должен сохраняться при столкновении. Энергия также почти сохраняется при условии, что не производится слишком много шума и тепла. 92$ и $2mv = nmu$. Нетрудно заметить, что единственным решением этих уравнений вместе является $n=2$ и $u=v$.

Более полный анализ исключил бы решения с разными шарами, летящими с разной скоростью, но я думаю, что этого достаточно, чтобы продемонстрировать принцип.

$\endgroup$

3

$\begingroup$

Начнем с наблюдения от бильярда. Допустим, красный шар неподвижен, и вы попали в него битком со скоростью $v$. Биток остановится, а красный шар продолжит движение со скоростью $v$. Любос дал хорошее и простое описание этого в своем ответе. Вы можете увидеть, как это происходит в начале этого видео.

Теперь представьте себе ряд шариков (скажем, красно-оранжево-желто-зелено-сине-фиолетовых), выстроенных идеально.

Вы попадаете кием точно в красный, кий останавливается и красный шар летит вперед.
Через мгновение красный шар ударяет по оранжевому шару. Красный останавливается, а оранжевый идет дальше. Затем оранжевый ударяется о желтый и останавливается и т. д. В конце концов фиолетовый шар выходит за линию, а все остальные шары в линии только что немного сдвинулись вниз по столу. Один мяч на входе, один мяч на выходе. Вы можете увидеть, как нечто подобное происходит через 50 секунд одного и того же видео (хотя оно не совсем идеально).

Теперь повторим. Выровняйте все шары, но на этот раз катите биток к красному шару, а сразу за ним катите шар с номером 8.

Биток ударяется о красный шар и останавливается; красный шар идет вперед, как и раньше. Красный мяч попадает в оранжевый мяч. На этот раз происходит не только это. Одновременно с этим столкновением шар-8 врезается в остановившийся биток. После этих столкновений в движении находятся два шара — оранжевый шар впереди и биток, который теперь имел два столкновения, одно спереди и одно сзади.

Этот процесс повторяется по линии, всегда с двумя движущимися мячами и одним неподвижным мячом между ними. Ближе к концу два движущихся шара — это фиолетовый (последний) шар и зеленый (третий от последнего) шар. Фиолетовый мяч свободен, но зеленый мяч ударяется о синий, и это последнее столкновение. В результате синие и фиолетовые шары уходят из строя. Все остальное остановлено. Два мяча вошли и два вышли.

Отсюда нетрудно увидеть, что мы можем отправить три, четыре или даже 100 шаров (теоретически) и снова получить то же самое число.

Трудность с этим объяснением заключается в том, что в колыбели Ньютона шары физически касаются друг друга, и поэтому аргумент «стоп-старт» не применим в той же мере. Этот простой анализ должен сделать колыбель Ньютона правдоподобной, но полный аргумент опирается на изучение механики континуума, связанной со столкновениями между твердыми телами. Эта статья, упомянутая Георгом в комментариях, содержит такой анализ.

Примечание: я не смотрел видео на YouTube полностью и не обязательно ручаюсь за все, что там говорится о физике. Я просто хотел примеры этих снимков. Кроме того, шары в бильярде катятся, что иногда может иметь значение по сравнению с колыбелью Ньютона, но здесь мы предполагаем, что это не так.

$\endgroup$

8

$\begingroup$

Во-первых, у меня есть бесплатное приложение для iPhone для колыбели Ньютона, которое называется Kinetic Balls и содержит около 500 скинов. 😉

События в колыбели состоят из множества шагов, хотя они происходят быстро друг за другом. В частности,

, если у вас есть пять мячей, первый мяч начинает с столкновения со вторым мячом, второй мяч касается третьего мяча, третий мяч касается четвертого мяча, четвертый мяч касается пятого мяча. ХОРОШО?

Итак, давайте изучим, что происходит, когда первый мяч слева попадает во второй мяч слева. Скорость первого мяча равна $v$ перед столкновением со вторым. Теперь проще взглянуть на столкновение из системы центра масс первых двух шаров.

Излишне говорить, что центр масс движется со скоростью, которая является средней скоростью первых двух (одинаково тяжелых) шаров. Поскольку первый движется на $v$ вправо, а второй имеет скорость, равную $0$, среднее значение равно $v/2$, хорошо?

Перед столкновением первый шарик движется со скоростью $v-v/2=v/2$ относительно центра масс, а второй шарик движется со скоростью $0-v/2=-v /2$ относительно центра масс.

Что происходит после столкновения? Шарики не могут проникнуть друг в друга, поэтому их относительная скорость должна изменить знак: скорости просто меняются местами. Они меняют знак. Ситуация полностью симметрична относительно обмена двумя шарами в сочетании с отражением «левого» и «правого» в пространстве. 2/2$. Знаки должны быть противоположны друг другу, но также и противоположны исходным, потому что шарики не могут проникать друг в друга.

Итак, в системе центра масс после столкновения левый шарик будет двигаться со скоростью $-v/2$, а правый шарик будет двигаться со скоростью $+v/2$. Преобразовываясь обратно из системы центра масс в модель лаборатории, мы должны снова добавить $v/2$. Таким образом, конечная скорость первого шара будет равна нулю, а конечная скорость второго шара будет равна $v/2+v/2=v$. ХОРОШО?

Теперь второй шарик приближается к третьему со скоростью $v$, пока третий шарик покоится. Возьмите опорную раму этих двух мячей.

Теперь повторите сказку выше четыре раза — я мог бы это сделать, это было бы очень увлекательно, но я хочу сохранить жесткие диски сервера — и вы получите ситуацию, в которой первые четыре шара находятся на отдыхает, а пятый движется со скоростью $v$ вправо.

$\endgroup$

4

$\begingroup$

Учитывая, что первоначальные шары не отскакивают назад, на первоначальный вопрос можно ответить напрямую, как показывает верхний ответ, но ему нужно было указать, что он предполагает, что другие мячи не отскакивают или иным образом не двигаются. Я могу объяснить это без математики: большее или меньшее количество шаров не может оторваться с более низкой или более высокой скоростью, потому что энергия и импульс должны сохраняться, а они являются разными функциями скорости. Если вы измените скорость и если другие шары не будут двигаться, то вы нарушите один из принципов сохранения. Например, если бы только 1 мяч оторвался с удвоенной скоростью, импульс был бы таким же (сохранялся), как у двух влетающих мячей, но в вылетающем мяче было бы в два раза больше энергии, чем в двух входящих мячах. И наоборот, если бы 4 шара оторвались со скоростью, равной 1/2 скорости, то импульс сохранился бы, но энергия была бы вдвое меньше, чем вложенная в него 9.0005

Однако гораздо труднее ответить на вопрос, разрешено ли другим шарам отскакивать в другом направлении.

Ответы, основанные на разделении, неверны, и один плакат намекнул на то, как на самом деле можно объяснить устройство. Только случайно расчет серии независимых ударов верен для нескольких шаров одинакового веса. Представьте себе 3 мяча, один из которых посередине намного тяжелее. Первый мяч отскочит, чего не происходит, когда они соприкасаются. Таким образом, расчет неверен по фундаментальной причине. Когда они соприкасаются, средний тяжелый мяч находится в сжатом состоянии, еще не отталкивая первый мяч, чтобы заставить его отскочить назад, прежде чем он отдаст энергию последнему мячу. Это не может быть смоделировано с одной ударной парой, за которой следует другая. Чтобы увидеть все более четко, смоделируйте шары как большие слабые пружины.

Из вики: «В точке столкновения распространяются две ударные волны, одна вперед и одна назад. Они несут всю кинетическую энергию ранее двигавшихся шаров в виде потенциальной энергии при упругом сжатии металла. Волна, идущая обратная отражается вперед, когда достигает начала цепочки шаров, приходя за волной, которая двигалась вперед первой Первая волна достигает конца и отражается назад и сталкивается с запаздывающей волной в точке, симметричной начальной точке столкновения, раздвигая шары, высвобождая потенциальную энергию в виде кинетической энергии. [8] Это объяснение более сложное, если шары одинакового веса имеют разную длину или если шары имеют разный вес, но решение для конечных скоростей может быть найдено путем изучения сжатия и расширения металлов в результате ударных волн Сохранение энергии и количества движения адекватно для объяснения системы, если потенциальная энергия и транс ионное время включено в расчеты сохранения энергии».

Теперь, чтобы ответить на исходный вопрос: как сказал другой постер, ударная волна встречается в точке, симметричной исходному столкновению. Однако ответ усложняется, если шары на конце имеют одинаковый вес, но разную длину. Ударные волны не встретятся с самого начала, но расширяющаяся система металла в конечном итоге заставит шары равного веса разделиться, так что первоначальные шары не отскочат назад.

Важное обновление/исправление:

Изучив это более подробно, я обнаружил, что никто не понимает, как работает подставка. Теория отраженной ударной волны исходит из:
http://www. {1.5}$, а не $F =кх$. Это дает набор взаимозависимых дифференциальных уравнений, которые я сформулирую в конце для наиболее общего случая различных масс и различных поверхностных упругих констант (модуль Юнга). Это может согласовываться с экспериментом для случая, когда 1 шар ударяет по 4, которые соприкасаются, но дает неверное решение для случая, когда 2 ударяют по 3. Я решил эту систему уравнений в Excel и получил тот же результат, что и в этой статье:
http://www.damtp.cam.ac.uk/user/hinch/publications/PRSLA455_3201.pdf
в котором скорости шаров 4 и 5 теоретически будут в 0,80 и 1,14 раза больше скорости двух влетающих шаров. В статье утверждается, что вы можете наблюдать разницу в скорости, но они не указывают, что это 2-кратная разница в кинетической энергии и, следовательно, высота, которую достигает 5-й шар, в 2 раза больше, чем 4-й, чего не происходит. вообще. (Если 5-й шар выходит максимум на 30 градусов, 4-й шар теоретически достигнет только 21 градуса, чего не происходит: они оба достигают 30 градусов одновременно).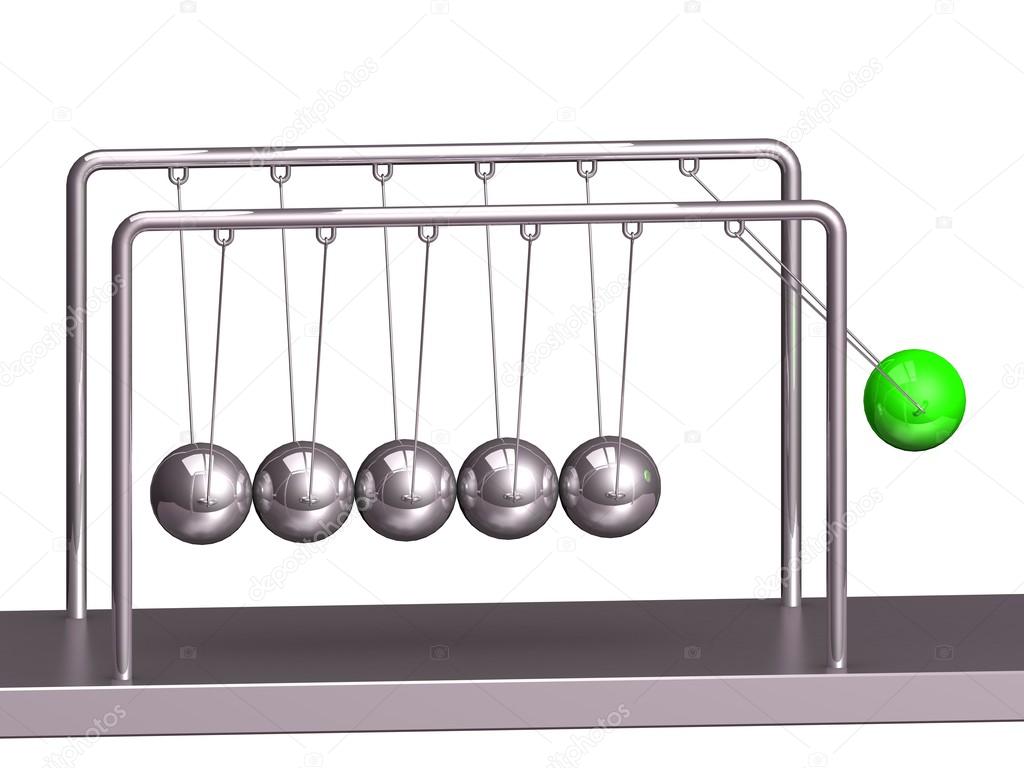
Вот уравнения $F=ma$, которые нужно решить с помощью Рунге-кутты, если теория Герца верна. Я делал это в Экселе. 9{1.5}
\end{align}$$

Для подключения к runge-kutta:
$$a=\frac{\mathrm dV(t)}{\mathrm dt}\ \text{and}\ x=tV(t)$$

$A, B, C, D$ — чистая эффективная пружина постоянная между каждой парой шариков для поверхностного сжатия.

Итак, когда 2 или более мячей ударяют друг друга, никто не знает, как это работает. Еще в 2004 году эти документы ошибочно назывались полным решением:
http://www.maths.tcd.ie/~garyd/Publications/Delaney_2004_AmJPhys_Rocking_Newtons_Cradle.pdf

$\endgroup$

2

$\begingroup$

Люди, отвечающие на подобные вопросы, совершают ужасную ошибку, возвращаясь к упрощенной математике из учебников по физике, забывая, что упрощенная математика не представляет ни атомных механизмов, ни того, как импульс работает в реальном мире.

Колыбель Ньютона заставляет нас задуматься о некоторых очень интересных следствиях физики в реальном мире. Тот факт, что в колыбели используются сферы, означает, например, что передача энергии происходит через точку контакта поверхности, которая (теоретически) стремится к нулю. Сферы предназначены для приближения к идеально эластичному материалу.

Вот вопрос. Что произойдет, если одну сферу в конце заменить сферой такого же размера и вдвое большей массы? Поднятие этого шара, безусловно, будет похоже на подъем двух обычных, но приведет ли столкновение к тому, что две сферы на другом конце оторвутся?

Решение кроется в теории волн (ударные волны распространяются по металлу так же, как звуковые волны по воздуху). Обычно столкновение n-шариков заставляет n-шариков подниматься на другом конце, потому что ударную волну можно представить как длину n-шариков, движущуюся вниз по ряду шаров после того, как произошло начальное столкновение. Важно отметить, что скорость столкновения шара всегда должна быть намного ниже скорости распространения ударной волны по металлу, чтобы люлька вел себя должным образом.

Возвращаясь к вопросу о более тяжелом шаре, в этом случае большая масса шара того же размера означает более высокую плотность, что изменит скорость, с которой ударная волна распространяется через материал. Что происходит, когда звуковая волна движется между материалами разной плотности? Высота тона и длина волны меняются. Тот же самый процесс дает нам преломление в призме волны, которая является светом.

На атомном уровне концепцию ударной волны будет трудно понять, поскольку в этом случае энергия входит в каждую новую сферу через крошечную точку контакта. «Ширина» энергии, движущейся по линии шаров, будет определять, сколько шаров улетит с другого конца, поскольку энергия по своей природе является кинетической. Инерция не позволяет кинетическому импульсу значительно сместить шары до тех пор, пока только крайние шары не будут обладать кинетической энергией и, таким образом, не смогут начать движение.

У каждого физика должна быть одна мантра, которую он повторяет снова и снова! «Модель не является реальностью». Модель — это математический инструмент, который мы создаем для предсказания поведения при определенных ограничениях (ограничениях, которые мы можем даже не понимать). Мы видим, как люди борются с проблемой колыбели Ньютона, потому что они упорно верят в то, что упрощенные модели никогда не должны заменяться более сложным пониманием. Только взгляните на эту чепуху, требующую, чтобы шарики имели минимальный зазор между собой, так что простую модель можно вообще применить. Посмотрите на дураков, которые думают, что это проблема n-шаров (не допускающих шаров разных размеров или плотности), как будто лежащая в основе физика имеет хоть какое-то отношение к макроколлекциям триллионов атомов в определенной форме, приятной Человеку.

Волновая теория лежит в основе современной физики. Люди, которые хотят созерцать динамику движущихся тел, всегда должны быть готовы перейти к более глубокому пониманию распространения энергии через различные материалы, когда проблема явно переключается с очень простых математических моделей на модели, которые должны учитывать лежащие в основе механизмы, вызванные природой. атомов (и их связей). Ньютоновская физика на макроуровне даст правильные решения только в том случае, если ключевые предположения останутся в силе. Колыбель Ньютона является примером эксперимента, в котором ньютоновская физика должна рассматриваться на атомном уровне (создание ударной волны). Математика макроуровня (очень упрощенная модель реальности) не даст правильных результатов. Взломать неправильную модель (требуя зазора в x микрон между шариками), чтобы попытаться заставить неправильную модель работать, может быть, в каком-то очень ограниченном наборе условий, является научным злодеянием.

$\endgroup$

Колыбель Ньютона — Мотивация

Устройство, которое вы видите, называется « Колыбель Ньютона «. Сборка, состоящая из 5 шаров, выстроенных в ряд. По какой-то причине это то, что мы видим в основном на рабочих столах. Я думаю, что те, кто кладет это на стол, дают понять, что если я справлюсь с этими 5 мячами, я справлюсь со всеми. Но может ли оно иметь другие значения помимо этого? Какую историю рассказывают нам эти крошечные сферы?

Колыбель Ньютона

Этот механизм назван в честь известного физика Исаака Ньютона. Хорошо бы ему такое изобрести, но не он изобрел. Это даже не было изобретено при его жизни. Точно неизвестно, кто первым изготовил этот инструмент. Но мы знаем, кто ее назвал, в 1967 году актер по имени Саймон Преббл назвал ее « Колыбель Ньютона». поднять первый шар в воздух, потенциальная энергия заряжена. Когда мы отпускаем, эта потенциальная энергия превращается в кинетическую энергию с эффектом гравитации, и она идет и касается второго шара. Импульс первого шара передается второму шару, которого он касается. Таким образом, импульс передается другим шарам по очереди и доходит до последнего шара. Последний шарик поднимается в результате передачи импульса и снова возвращается и касается предыдущего шарика.

Так мы физически объяснили, что происходит. В том, что все? Не может ли эта информация раскрыть другие значения в нашем сознании? Например, когда я смотрю на эти сферы, я вижу цепочку движения и изменения. Точно так же, как мы замечаем, когда смотрим вокруг себя. Мы видим, что вещи постоянно меняются. Эти изменения не происходят автоматически. Для того, чтобы этот шар изменил свое положение, другой шар должен сначала изменить свое положение. Как я уже сказал, это цепь движения и изменения.

Если мы не удовлетворены нашей текущей ситуацией; Если мы хотим изменить себя, свою жизнь и окружающую среду, мы должны изучать законы физики с другой точки зрения. Чтобы принять меры, мы должны выслушать историю этих крошечных сфер.

Давайте посмотрим на законы движения Ньютона. Исаак Ньютон, более известный как физик, опубликовал одну из самых важных научных книг в истории в 1687 году: Эта книга под названием « Philosophiæ Naturalis Principia Mathematica » заложила основу классической механики. У книги восхитительное название, но почему-то большинство людей сосредотачивается на второй половине названия, на стороне «математических принципов». Однако полное название книги — « Математические принципы натуральной философии 9».0043 .» Тогда давайте попробуем прочесть смысл натурфилософии, начиная с математических принципов. Попробуем применить математику и физику к нашей собственной жизни.

Даже самый маленький предмет, который вы видите в мире, не хочет менять своего положения, своего текущее состояние. Он не хочет двигаться. Он ленив. Поставьте себя на место «объекта» в этом предложении. Объект — это вы.

Объекты хотят оставаться такими, какие они есть. Это также первый из законы движения, открытые Ньютоном.Даже самый маленький объект в этой вселенной не движется застойно.Он сохраняет состояние бездействия.Пока на него не действует внешняя сила.Как только вы прикладываете эту внешнюю силу,он начинает действовать и на этот раз он пытается сохранить свою подвижность.Теоретически он будет продолжать это движение бесконечно.Например, если вы ударите такой объект в пространстве, он будет продолжать свой путь без остановки. Но в мире все иначе.Здесь как всегда, есть внешние силы. ой это останавливает это. Сила трения в воздухе или на земле или другие вещи препятствуют этой подвижности. Таким образом, мы можем лучше понять 1-й закон Ньютона. Объекты хотят сохранить свои существующие позиции, и снова объекты хотят продолжать делать то, что они делали раньше, объекты. Как я уже сказал, они ленивы. Но, к счастью, ученые смогли более мягко выразить эту лень и назвали ее «бездействием».

Бездействие — часть нашей жизни. Нелегко действовать. Сделать первый шаг всегда сложно. Но как только вы сделаете этот шаг, все станет проще. Вы набираете обороты. Вы начинаете поддерживать этот импульс. Тик-так, тик-так. Вы почти синхронизированы со временем.

Не всегда ждите, пока такая внешняя сила начнет действовать. Эта сила, в которой вы нуждаетесь, всегда «потенциально» находится внутри вас. Находите ли вы теперь эту силу в крови, в ваших венах, в складках вашего мозга, которые ее питают, или в вашем сердце, которое ее качает? Вы решаете это. В конце концов, вы должны поднять этот первый мячик в воздух, чтобы превратить потенциал внутри вас в кинетическую энергию. Итак, повторим первый закон.

Первый закон Ньютона: закон инерции.

«Закон I: Все тела имеют равномерное прямолинейное движение, если они не вынуждены изменить свое состояние под действием силы.

Сила очень важна. Итак, что еще мы можем узнать об этой силе из физики и математики? Для этого нам придется обратиться ко второму закону. Одна из важнейших формул в истории науки…

F = м.д.

Мы можем прочитать эту формулу следующим образом: «Ускорение объекта прямо пропорционально приложенной к нему силе и обратно пропорционально массе объекта». Итак, кто является дополнением в этом предложении? Мы. Мы сами. Если мы хотим ускориться, если мы хотим увеличить имеющуюся у нас скорость, мы либо уменьшим свою массу, то есть ослабим, либо увеличим свою силу.

Второй закон Ньютона: известен как закон ускорения.

«Lex II: Mutationem motus пропорциональна esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur…»

«Закон II: изменение импульса объекта пропорционально тяге, действующей на объект и происходит вдоль прямой линии, по которой приложена тяга».

Независимо от того, приложена ли сила сразу или постепенно, если она вызывает движение, другая сила, вдвое превышающая эту силу, удвоит движение, а сила, втрое превышающая силу, утроит движение. И это движение суммируется с предыдущим движением, если предмет двигался раньше, в том же направлении, что и предыдущее движение.

Теперь давайте применим то, что мы узнали из физики, к нашей жизни. Чтобы наблюдать ускоряющиеся изменения в нашей жизни, нам нужно направить нашу силу воли к цели и постоянно прилагать ее в этом направлении. Просто делать что-то недостаточно, чтобы избавиться от бездействия. Быть быстрым в одиночку необходимо, но недостаточно, чтобы добраться из одной точки в другую. Чтобы ускориться, нам нужно направление. Отсюда сосредоточенная сила.

А когда мы направляем все свои силы и силу воли на достижение определенной цели, к сожалению, работа не заканчивается. Перед нами препятствия. Реакции на эффект, который мы начали создавать, начинают проявляться. Что приводит нас к третьему закону Ньютона:

Третий закон Ньютона: закон действия-противодействия

«Закон III: на каждую силу всегда существует равная и противоположно направленная сила противодействия: или силы, действующие между двумя телами друг на друга, всегда имеют одинаковое и противоположное направление».

Третий закон Ньютона говорит нам, что все силы взаимодействуют друг с другом. Так что нет такой вещи, как однонаправленная сила. Когда вы начинаете что-то делать, используя силу воли внутри нас, вы обязательно сначала создадите себе препятствия. «Машина оправданий» внутри вас заработает и скажет вам: «У тебя нет времени», «Ты опять потерпишь неудачу», «Ты все равно не талантлив!» Допустим, вы заставили их замолчать. На этот раз начнутся реакции окружающей среды. В конце концов, для тебя есть роль. Зачем пытаться ускориться, если в этой роли можно двигаться вперед с постоянной скоростью? Вы пытаетесь оказать влияние своей силой воли?

Мы уже знаем, что даже если вы ударите камень о землю, он окажет на вас равную и противоположную силу. Тогда совершенно нормально сталкиваться с такими реакциями внутри и снаружи. Даже противоположное противоречит характеру бизнеса. Если мы примем это как таковое, не укрепится ли наша воля к увеличению нашей силы?

Как тело, мы знаем, что для того, чтобы действовать, мы должны сначала возвыситься. Несмотря на гравитацию. Несмотря на сопротивление воздуха. Мы можем достичь этого, если усилим в себе силу воли. Опять же, как объект, мы знаем, что потенциальная энергия внутри нас проявляется только таким образом. Конечно, будут реакции. Нам может противостоять один человек, два человека или трое. Он может не захотеть двигаться. Но будьте уверены, что четвертый человек будет действовать под вашим влиянием.